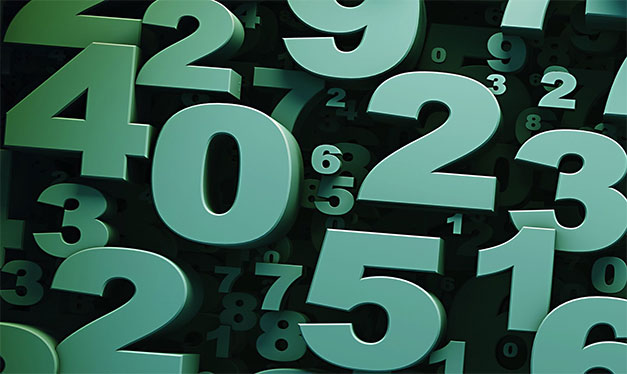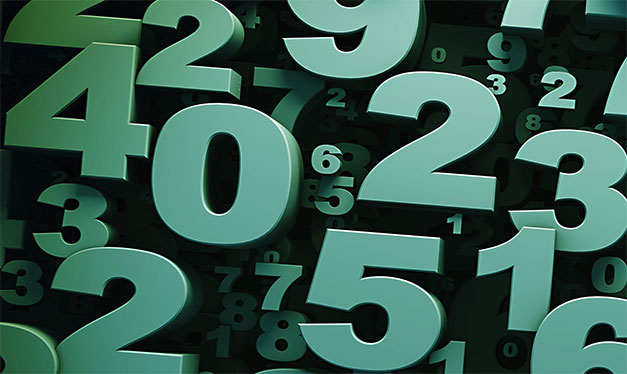Math.random()

Композиция генераторов

Композиция генераторов – это особенная возможность генераторов, которая позволяет прозрачно «встраивать» генераторы друг в друга.

Например, у нас есть функция для генерации последовательности чисел:

Мы хотели бы использовать её при генерации более сложной последовательности:

сначала цифры (с кодами символов 48…57)
за которыми следуют буквы в верхнем регистре (коды символов 65…90)
за которыми следуют буквы алфавита (коды символов 97…122)

Мы можем использовать такую последовательность для генерации паролей, выбирать символы из неё (может быть, ещё добавить символы пунктуации), но сначала её нужно сгенерировать.

В обычной функции, чтобы объединить результаты из нескольких других функций, мы вызываем их, сохраняем промежуточные результаты, а затем в конце их объединяем.

Для генераторов есть особый синтаксис , который позволяет «вкладывать» генераторы один в другой (осуществлять их композицию).

Вот генератор с композицией:

Директива делегирует выполнение другому генератору. Этот термин означает, что перебирает генератор и прозрачно направляет его вывод наружу. Как если бы значения были сгенерированы внешним генератором.

Результат – такой же, как если бы мы встроили код из вложенных генераторов:

Композиция генераторов – естественный способ вставлять вывод одного генератора в поток другого. Она не использует дополнительную память для хранения промежуточных результатов.

Плоский асинхронный код

Class random

Одна из основных областей применения генераторов – написание «плоского» асинхронного кода.

Общий принцип такой:

Генератор не просто значения, а промисы.
Есть специальная «функция-чернорабочий» которая запускает генератор, последовательными вызовами получает из него промисы – один за другим, и, когда очередной промис выполнится, возвращает его результат в генератор следующим .
Последнее значение генератора () уже обрабатывает как окончательный результат – например, возвращает через промис куда-то ещё, во внешний код или просто использует, как в примере ниже.

Напишем такой код для получения аватара пользователя с github и его вывода, аналогичный рассмотренному в статье про промисы.

Для AJAX-запросов будем использовать метод fetch, он как раз возвращает промисы.

Функция в примере выше – универсальная, она может работать с любым генератором, который промисы.

Вместе с тем, это – всего лишь набросок, чтобы было понятно, как такая функция в принципе работает. Есть уже готовые реализации, обладающие большим количеством возможностей.

Одна из самых известных – это библиотека co, которую мы рассмотрим далее.

Перебор генераторов

Math.floor()

Как вы, наверное, уже догадались по наличию метода , генераторы являются перебираемыми объектами.

Возвращаемые ими значения можно перебирать через :

Выглядит гораздо красивее, чем использование , верно?

…Но обратите внимание: пример выше выводит значение , затем. Значение выведено не будет!. Это из-за того, что перебор через игнорирует последнее значение, при котором

Поэтому, если мы хотим, чтобы были все значения при переборе через , то надо возвращать их через :

Это из-за того, что перебор через игнорирует последнее значение, при котором . Поэтому, если мы хотим, чтобы были все значения при переборе через , то надо возвращать их через :

Так как генераторы являются перебираемыми объектами, мы можем использовать всю связанную с ними функциональность, например оператор расширения :

В коде выше превращает перебираемый объект-генератор в массив элементов (подробнее ознакомиться с оператором расширения можно в главе )

Extending

Math

You can add your own methods to instances, as such:

var random = new Random();
random.bark = function() {
  if (this.bool()) {
    return "arf!";
  } else {
    return "woof!";
  }
};
random.bark(); //=> "arf!" or "woof!"

This is the recommended approach, especially if you only use one instance of .

Or you could even make your own subclass of Random:

function MyRandom(engine) {
  return Random.call(this, engine);
}
MyRandom.prototype = Object.create(Random.prototype);
MyRandom.prototype.constructor = MyRandom;
MyRandom.prototype.mood = function() {
  switch (this.integer(, 2)) {
    case :
      return "Happy";
    case 1:
      return "Content";
    case 2:
      return "Sad";
  }
};
var random = new MyRandom();
random.mood(); //=> "Happy", "Content", or "Sad"

Or, if you have a build tool are are in an ES6+ environment:

class MyRandom extends Random {
  mood() {
    switch (this.integer(, 2)) {
      case :
        return "Happy";
      case 1:
        return "Content";
      case 2:
        return "Sad";
    }
  }
}
const random = new MyRandom();
random.mood(); //=> "Happy", "Content", or "Sad"

generator.throw

Как мы видели в примерах выше, внешний код может передавать значение в генератор как результат .

…Но можно передать не только результат, но и инициировать ошибку. Это естественно, так как ошибка является своего рода результатом.

Для того, чтобы передать ошибку в , нам нужно вызвать . В таком случае исключение возникнет на строке с .

Например, здесь приведёт к ошибке:

Ошибка, которая проброшена в генератор на строке , приводит к исключению на строке с . В примере выше перехватывает её и отображает.

Если мы не хотим перехватывать её, то она, как и любое обычное исключение, «вывалится» из генератора во внешний код.

Текущая строка вызывающего кода – это строка с , отмечена . Таким образом, мы можем отловить её во внешнем коде, как здесь:

Если же ошибка и там не перехвачена, то дальше – как обычно, она выпадает наружу и, если не перехвачена, «повалит» скрипт.

How does Random.js alleviate these problems?

Random.js provides a set of «engines» for producing random integers, which consistently provide values within , i.e. 32 bits of randomness.

One is also free to implement their own engine as long as it returns 32-bit integers, either signed or unsigned.

Some common, biased, incorrect tool for generating random integers is as follows:

The problem with both of these approaches is that the distribution of integers that it returns is not uniform. That is, it might be more biased to return rather than , making it inherently broken.

may more evenly distribute its biased, but it is still wrong. , at least in the example given, is heavily biased to return over .

In order to eliminate bias, sometimes the engine which random data is pulled from may need to be used more than once.

Random.js provides a series of distributions to alleviate this.

Функция-генератор

Для объявления генератора используется специальная синтаксическая конструкция: , которая называется «функция-генератор».

Выглядит она так:

Функции-генераторы ведут себя не так, как обычные. Когда такая функция вызвана, она не выполняет свой код. Вместо этого она возвращает специальный объект, так называемый «генератор», для управления её выполнением.

Вот, посмотрите:

Выполнение кода функции ещё не началось:

Основным методом генератора является . При вызове он запускает выполнение кода до ближайшей инструкции (значение может отсутствовать, в этом случае оно предполагается равным ). По достижении выполнение функции приостанавливается, а соответствующее значение – возвращается во внешний код:

Результатом метода всегда является объект с двумя свойствами:

: значение из .
: , если выполнение функции завершено, иначе .

Например, здесь мы создаём генератор и получаем первое из возвращаемых им значений:

На данный момент мы получили только первое значение, выполнение функции остановлено на второй строке:

Повторный вызов возобновит выполнение кода и вернёт результат следующего :

И, наконец, последний вызов завершит выполнение функции и вернёт результат :

Сейчас генератор полностью выполнен. Мы можем увидеть это по свойству и обработать как окончательный результат.

Новые вызовы больше не имеют смысла. Впрочем, если они и будут, то не вызовут ошибки, но будут возвращать один и тот же объект: .

или ?

Нет разницы, оба синтаксиса корректны.

Но обычно предпочтителен первый вариант, так как звёздочка относится к типу объявляемой сущности ( – «функция-генератор»), а не к её названию, так что резонно расположить её у слова .

Usage

In your project, run the following command:

npm install random-js

yarn add random-js

In your code:

import{Random}from"random-js";constrandom=newRandom();constvalue=random.integer(1,100);

const{Random}=require("random-js");constrandom=newRandom();constvalue=random.integer(1,100);

Or to have more control:

constRandom=require("random-js").Random;constrandom=newRandom(MersenneTwister19937.autoSeed());constvalue=random.integer(1,100);

It is recommended to create one shared engine and/or instance per-process rather than one per file.

Download and place it in your project, then use one of the following patterns:

define(function(require){var Random =require("random");returnnewRandom.Random(Random.MersenneTwister19937.autoSeed());});define(function(require){var Random =require("random");returnnewRandom.Random();});define("random",function(Random){returnnewRandom.Random(Random.MersenneTwister19937.autoSeed());});

Download and place it in your project, then add it as a tag as such:

<scriptsrc="lib/random-js.min.js"><script><script>var random =newRandom.Random();alert("Random value from 1 to 100: "+random.integer(1,100));</script>

Неточные вычисления

Внутри JavaScript число представлено в виде 64-битного формата IEEE-754. Для хранения числа используется 64 бита: 52 из них используется для хранения цифр, 11 из них для хранения положения десятичной точки (если число целое, то хранится 0), и один бит отведён на хранение знака.

Если число слишком большое, оно переполнит 64-битное хранилище, JavaScript вернёт бесконечность:

Наиболее часто встречающаяся ошибка при работе с числами в JavaScript – это потеря точности.

Посмотрите на это (неверное!) сравнение:

Да-да, сумма и не равна .

Странно! Что тогда, если не ?

Но почему это происходит?

Число хранится в памяти в бинарной форме, как последовательность бит – единиц и нулей. Но дроби, такие как , , которые выглядят довольно просто в десятичной системе счисления, на самом деле являются бесконечной дробью в двоичной форме.

Другими словами, что такое ? Это единица делённая на десять — , одна десятая. В десятичной системе счисления такие числа легко представимы, по сравнению с одной третьей: , которая становится бесконечной дробью .

Деление на гарантированно хорошо работает в десятичной системе, но деление на – нет. По той же причине и в двоичной системе счисления, деление на обязательно сработает, а становится бесконечной дробью.

В JavaScript нет возможности для хранения точных значений 0.1 или 0.2, используя двоичную систему, точно также, как нет возможности хранить одну третью в десятичной системе счисления.

Числовой формат IEEE-754 решает эту проблему путём округления до ближайшего возможного числа. Правила округления обычно не позволяют нам увидеть эту «крошечную потерю точности», но она существует.

Пример:

И когда мы суммируем 2 числа, их «неточности» тоже суммируются.

Вот почему – это не совсем .

Не только в JavaScript

Справедливости ради заметим, что ошибка в точности вычислений для чисел с плавающей точкой сохраняется в любом другом языке, где используется формат IEEE 754, включая PHP, Java, C, Perl, Ruby.

Можно ли обойти проблему? Конечно, наиболее надёжный способ — это округлить результат используя метод toFixed(n):

Также можно временно умножить число на 100 (или на большее), чтобы привести его к целому, выполнить математические действия, а после разделить обратно. Суммируя целые числа, мы уменьшаем погрешность, но она все равно появляется при финальном делении:

Таким образом, метод умножения/деления уменьшает погрешность, но полностью её не решает.

Забавный пример

Попробуйте выполнить его:

Причина та же – потеря точности. Из 64 бит, отведённых на число, сами цифры числа занимают до 52 бит, остальные 11 бит хранят позицию десятичной точки и один бит – знак. Так что если 52 бит не хватает на цифры, то при записи пропадут младшие разряды.

Интерпретатор не выдаст ошибку, но в результате получится «не совсем то число», что мы и видим в примере выше. Как говорится: «как смог, так записал».

Два нуля

Другим забавным следствием внутреннего представления чисел является наличие двух нулей: и .

Все потому, что знак представлен отдельным битом, так что, любое число может быть положительным и отрицательным, включая нуль.

В большинстве случаев это поведение незаметно, так как операторы в JavaScript воспринимают их одинаковыми.

Создание генератора

Для объявления генератора используется новая синтаксическая конструкция: (функция со звёздочкой).

Её называют «функция-генератор» (generator function).

Выглядит это так:

При запуске код такой функции не выполняется. Вместо этого она возвращает специальный объект, который как раз и называют «генератором».

Правильнее всего будет воспринимать генератор как «замороженный вызов функции»:

При создании генератора код находится в начале своего выполнения.

Основным методом генератора является . При вызове он возобновляет выполнение кода до ближайшего ключевого слова . По достижении выполнение приостанавливается, а значение – возвращается во внешний код:

Повторный вызов возобновит выполнение и вернёт результат следующего :

И, наконец, последний вызов завершит выполнение функции и вернёт результат :

Функция завершена. Внешний код должен увидеть это из свойства и обработать , как окончательный результат.

«Открутить назад» завершившийся генератор нельзя, но можно создать новый ещё одним вызовом и выполнить его.

или ?

Можно ставить звёздочку как сразу после , так и позже, перед названием. В интернете можно найти обе эти формы записи, они верны:

Технически, нет разницы, но писать то так то эдак – довольно странно, надо остановиться на чём-то одном.

Автор этого текста полагает, что правильнее использовать первый вариант , так как звёздочка относится к типу объявляемой сущности ( – «функция-генератор»), а не к её названию. Конечно, это всего лишь рекомендация-мнение, не обязательное к выполнению, работать будет в любом случае.

Why is this needed?

Despite being capable of producing numbers within [0, 1), there are a few downsides to doing so:

It is inconsistent between engines as to how many bits of randomness:
- Internet Explorer: 53 bits
- Mozilla Firefox: 53 bits
- Google Chrome/node.js: 32 bits
- Apple Safari: 32 bits
It is non-deterministic, which means you can’t replay results consistently
In older browsers, there can be manipulation through cross-frame random polling. This is mostly fixed in newer browsers and is required to be fixed in ECMAScript 6.

Also, and most crucially, most developers tend to use improper and biased logic as to generating integers within a uniform distribution.

1 Псевдослучайные числа

Иногда программист сталкивается с простыми, казалось бы, задачами: «отобрать случайный фильм для вечернего просмотра из определенного списка», «выбрать победителя лотереи», «перемешать список песен при тряске смартфона», «выбрать случайное число для шифрования сообщения», и каждый раз у него возникает очень закономерный вопрос: а как получить это самое случайное число?

Вообще-то, если вам нужно получить «настоящее случайное число», сделать это довольно-таки трудно. Вплоть до того, что в компьютер встраивают специальные математические сопроцессоры, которые умеют генерировать такие числа, с выполнением всех требований к «истинной случайности».

Поэтому программисты придумали свое решение — псевдослучайные числа. Псевдослучайные числа — это некая последовательность, числа в которой на первый взгляд кажутся случайными, но специалист при детальном анализе сможет найти в них определенные закономерности. Для шифрования секретных документов такие числа не подойдут, а для имитации бросания кубика в игре — вполне.

Есть много алгоритмов генерации последовательности псевдослучайных чисел и почти все из них генерируют следующее случайное число на основе предыдущего и еще каких-то вспомогательных чисел.

Например, данная программа выведет на экран неповторяющихся чисел:

Кстати, мы говорим не о псевдослучайных числах, а именно о последовательности таких чисел. Т.к. глядя на одно число невозможно понять, случайное оно или нет.

Случайное число ведь можно получить разными способами:

Генератор псевдослучайных чисел и генератор случайных чисел

Для того, чтобы получить что-то случайное, нам нужен источник энтропии, источник некого хаоса из который мы будем использовать для генерации случайности.

Этот источник используется для накопления энтропии с последующим получением из неё начального значения (initial value, seed), которое необходимо генераторам случайных чисел (ГСЧ) для формирования случайных чисел.

Генератор ПсевдоСлучайных Чисел использует единственное начальное значение, откуда и следует его псевдослучайность, в то время как Генератор Случайных Чисел всегда формирует случайное число, имея в начале высококачественную случайную величину, которая берется из различных источников энтропии.

Выходит, что чтобы создать псевдослучайную последовательность нам нужен алгоритм, который будет генерить некоторую последовательность на основании определенной формулы. Но такую последовательность можно будет предсказать. Тем не менее, давайте пофантазируем, как бы могли написать свой генератор случайных чисел, если бы у нас не было Math.random()

ГПСЧ имеет некоторый алгоритм, который можно воспроизвести.
ГСЧ — это получение чисел полностью из какого либо шума, возможность просчитать который стремится к нулю. При этом в ГСЧ есть определенные алгоритмы для выравнивания распределения.

Генератор – итератор

Как вы, наверно, уже догадались по наличию метода , генератор связан с итераторами. В частности, он является итерируемым объектом.

Его можно перебирать и через :

Заметим, однако, существенную особенность такого перебора!

При запуске примера выше будет выведено значение , затем . Значение выведено не будет. Это потому что стандартный перебор итератора игнорирует на последнем значении, при . Так что результат в цикле не выводится.

Соответственно, если мы хотим, чтобы все значения возвращались при переборе через , то надо возвращать их через :

…А зачем вообще при таком раскладе, если его результат игнорируется? Он тоже нужен, но в других ситуациях. Перебор через – в некотором смысле «исключение». Как мы увидим дальше, в других контекстах очень даже востребован.

Способы записи числа

Представьте, что нам надо записать число 1 миллиард. Самый очевидный путь:

Но в реальной жизни мы обычно опускаем запись множества нулей, так как можно легко ошибиться. Укороченная запись может выглядеть как или для 7 миллиардов 300 миллионов. Такой принцип работает для всех больших чисел.

В JavaScript можно использовать букву , чтобы укоротить запись числа. Она добавляется к числу и заменяет указанное количество нулей:

Другими словами, производит операцию умножения числа на 1 с указанным количеством нулей.

Сейчас давайте запишем что-нибудь очень маленькое. К примеру, 1 микросекунду (одна миллионная секунды):

Записать микросекунду в укороченном виде нам поможет .

Если мы подсчитаем количество нулей , их будет 6. Естественно, верная запись .

Другими словами, отрицательное число после подразумевает деление на 1 с указанным количеством нулей:

Шестнадцатеричные числа широко используются в JavaScript для представления цветов, кодировки символов и многого другого. Естественно, есть короткий стиль записи: , после которого указывается число.

Например:

Не так часто используются двоичные и восьмеричные числа, но они также поддерживаются для двоичных и для восьмеричных:

Есть только 3 системы счисления с такой поддержкой. Для других систем счисления мы рекомендуем использовать функцию (рассмотрим позже в этой главе).

Extending

You can add your own methods to instances, as such:

var random =newRandom();random.bark=function(){if(this.bool()){return"arf!";}else{return"woof!";}};random.bark();

This is the recommended approach, especially if you only use one instance of .

Or you could even make your own subclass of Random:

functionMyRandom(engine){returnRandom.call(this, engine);}MyRandom.prototype=Object.create(Random.prototype);MyRandom.prototype.constructor= MyRandom;MyRandom.prototype.mood=function(){switch(this.integer(,2)){casereturn"Happy";case1return"Content";case2return"Sad";}};var random =newMyRandom();random.mood();

Or, if you have a build tool are are in an ES6+ environment:

classMyRandomextendsRandom{mood(){switch(this.integer(,2)){casereturn"Happy";case1return"Content";case2return"Sad";}}}constrandom=newMyRandom();random.mood();

Alternate API

There is an alternate API which may be easier to use, but may be less performant. In scenarios where performance is paramount, it is recommended to use the aforementioned API.

constrandom=newRandom(MersenneTwister19937.seedWithArray(0x12345678,0x90abcdef));constvalue=r.integer(,99);constotherRandom=newRandom();

This abstracts the concepts of engines and distributions.

: Produce an integer within the inclusive range . can be at its minimum -9007199254740992 (2 ** 53). can be at its maximum 9007199254740992 (2 ** 53). The special number is never returned.
: Produce a floating point number within the range . Uses 53 bits of randomness.
: Produce a boolean with a 50% chance of it being .
: Produce a boolean with the specified chance causing it to be .
: Produce a boolean with / chance of it being true.
: Return a random value within the provided within the sliced bounds of and .
: Shuffle the provided (in-place). Similar to .
: From the array, produce an array with elements that are randomly chosen without repeats.
: Same as
: Produce an array of length with as many rolls.
: Produce a random string using numbers, uppercase and lowercase letters, , and of length .
: Produce a random string using the provided string as the possible characters to choose from of length .
or : Produce a random string comprised of numbers or the characters of length .
: Produce a random string comprised of numbers or the characters of length .
: Produce a random within the inclusive range of . and must both be s.

Usage

ES6

Each method has signature, where is optional.

import {
  generateIntegers,
  generateDecimalFractions,
  generateGaussians,
  generateStrings,
  generateUUIDs,
  generateBlobs,
  getUsage,
  generateSignedIntegers,
  generateSignedDecimalFractions,
  generateSignedGaussians,
  generateSignedStrings,
  generateSignedUUIDs,
  generateSignedBlobs,
  verifySignature,

  // special
  request,
  RandomOrg
} from 'randomorg-js'

CommonJS / Node.JS

Notice that Node > 4 is required for feature.

const {
  generateIntegers,
  generateDecimalFractions,
  generateGaussians,
  generateStrings,
  // ...
  generateSignedBlobs,
  verifySignature,

  // special
  request,
  RandomOrg
} = require('randomorg-js')

So you simply can just use old way

var randomorg = require('randomorg-js')

console.log(randomorg)
console.log(randomorg.generateIntegers)
console.log(randomorg.generateDecimalFractions)
console.log(randomorg.verifySignature)
console.log(randomorg.request)
console.log(randomorg.RandomOrg)
// and etc.

Example

const params = {
  apiKey: 'your api key',
  n: 6,
  min: 1,
  max: 6
}

generateIntegers(params, (err, response) => {
  // there may have `err` or `response.error`
  console.log(err || response.error)

  // response is exactly what the API spec
  // defines as response object
  console.log(response)
  console.log(response.id)
  console.log(response.result)
})

Or using the method

request('generateSignedStrings', {
  n: 8,
  length: 10,
  characters: 'ab!~cdefg+_-hijk@lmn#$%opqr^stuvwxyz',
}, (err, response) => {
  console.log(err, response)
})

By default the package exports all methods with randomly generated . To change that, the onoe way can be to add as first argument to each method e.g. ; or the second variant is to call the which returns the same methods and they will use the defined from the constructor.

const { RandomOrg } = require('randomorg-js')

const random = RandomOrg(123555)

random.generateSignedBlobs({
 apiKey: 'your api key here',
 and: 'other params for that method'
}, (er, { id, result }) => {
  // response always has the same ID what
  // user has provided
  console.log(id) // => 123555
  console.log(result) // => random Signed Blobs
})

// but you still can provide
// different `id` to same method
random.generateSignedBlobs(4444, params, (e, { id }) => {
  console.log(id) // => 4444
})

// or to some other method
random.generateIntegers(2938742, params, (e, { id }) => {
  console.log(id) // => 2938742
})

Предсказываем Math.random()

В нем есть задача:

Что нужно вписать вместо вопросов, чтобы функция вернула true? Кажется что это невозможно. Но, это возможно, если вы заглядывали в спеку и видели алгоритм ГПСЧ V8. Решение этой задачи в свое время мне показал Роман Дворнов:

Этот код работал в 70% случаев для Chrome < 49 и Node.js < 5. Рома Дворнов, как всегда, показал чудеса магии, которая не что иное, как глубокое понимание внутренних механизмов браузеров. Я все жду, когда Роман сделает доклад на основе этих событий или напишет более подробную статью.

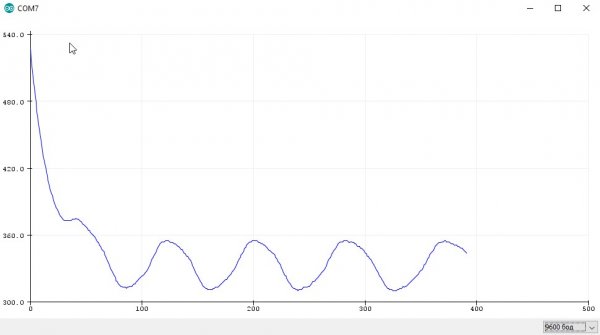
Видите эти равномерности на левом слайде? Изображение показывает проблему с распределением значений. На картинке слева видно, что значения местами сильно группируются, а местами выпадают большие фрагменты. Как следствие — числа можно предсказать.

Выходит что мы можем отреверсить Math.random() и предсказать, какое было загадано число на основе того, что получили в данный момент времени. Для этого получаем два значения через Math.random(). Затем вычисляем внутреннее состояние по этим значениям. Имея внутреннее состояние можем предсказывать следующие значения Math.random() при этом не меняя внутреннее состояние. Меняем код так так, чтобы вместо следующего возвращалось предыдущее значение. Собственно все это и описано в коде-решении для задачи random4. Но потом алгоритм изменили (подробности читайте в спеке). Его можно будет сломать, как только у нас в JS появится нормальная работа с 64 битными числами. Но это уже будет другая история.

Новый алгоритм выглядит так:

Его все так же можно будет просчитать и предсказать. Но пока у нас нет “длинной математики” в JS. Можно попробовать через TypedArray сделать или использовать специальные библиотеки. Возможно кто-то однажды снова напишет предсказатель. Возможно это будешь ты, читатель. Кто знает 😉

Округление

Одна из часто используемых операций при работе с числами – это округление.

В JavaScript есть несколько встроенных функций для работы с округлением:

Округление в меньшую сторону: становится , а — .; Округление в большую сторону: становится , а — .; Округление до ближайшего целого: становится , — , а — .
(не поддерживается в Internet Explorer): Производит удаление дробной части без округления: становится , а — .

Ниже представлена таблица с различиями между функциями округления:

Эти функции охватывают все возможные способы обработки десятичной части. Что если нам надо округлить число до количества цифр в дробной части?

Например, у нас есть и мы хотим округлить число до 2-х знаков после запятой, оставить только .

Есть два пути решения:

Умножить и разделить.
Например, чтобы округлить число до второго знака после запятой, мы можем умножить число на , вызвать функцию округления и разделить обратно.

Метод toFixed(n) округляет число до знаков после запятой и возвращает строковое представление результата.

Округляет значение до ближайшего числа, как в большую, так и в меньшую сторону, аналогично методу :

Обратите внимание, что результатом является строка. Если десятичная часть короче, чем необходима, будут добавлены нули в конец строки:

Мы можем преобразовать полученное значение в число, используя унарный оператор или , пример с унарным оператором: .

toString(base)

Метод возвращает строковое представление числа в системе счисления .

Например:

может варьироваться от до (по умолчанию ).

Часто используемые:

base=16 — для шестнадцатеричного представления цвета, кодировки символов и т.д., цифры могут быть или .
base=2 — обычно используется для отладки побитовых операций, цифры или .
base=36 — максимальное основание, цифры могут быть или . То есть, используется весь латинский алфавит для представления числа. Забавно, но можно использовать -разрядную систему счисления для получения короткого представления большого числового идентификатора. К примеру, для создания короткой ссылки. Для этого просто преобразуем его в -разрядную систему счисления:

Две точки для вызова метода

Внимание! Две точки в это не опечатка. Если нам надо вызвать метод непосредственно на числе, как в примере выше, то нам надо поставить две точки после числа

Если мы поставим одну точку: , тогда это будет ошибкой, поскольку синтаксис JavaScript предполагает, что после первой точки начинается десятичная часть. А если поставить две точки, то JavaScript понимает, что десятичная часть отсутствует, и начинается метод.

Также можно записать как .

Класс Random

В качестве генератора псевдослучайных чисел можно также использовать класс java.util.Random, имеющий два
конструктора :

public Random();
public Random(long);

Поскольку Random создаёт псевдослучайное число, то определив начальное число, устанавливается начальная точка
случайной последовательности, способствующая получению одинаковых случайных последовательностей. Чтобы избежать такого
совпадения, обычно применяют второй конструктор с использованием в качестве инициирующего значения текущего времени.
В таблице представлены наиболее часто используемые методы генератора Random :

Метод	Описание
boolean nextBoolean()	получение следующего случайного значения типа boolean
double nextDouble()	получение следующего случайного значения типа double
float nextFloat()	получение следующего случайного значения типа float
int nextInt()	получение следующего случайного значения типа int
int nextInt(int n)	получение следующего случайного значения типа int в диапазоне от 0 до n
long nextLong()	получение следующего случайного значения типа long
void nextBytes(byte[] buf)	формирование массива из случайно генерируемых значений

Пример получения псевдослучайного целочисленного значения с использованием класса Random :

Random random = new Random();

int i = random.nextInt();

С классом Random алгоритм получения псевдослучайного числа такой же, как и у метода random класса
Math. Допустим, что нам необходимо получить случайное число в диапазоне , 100 включительно. В этом случае
код может выглядеть следующим образом :

int min = 5;
int max = 100;
int diff = max - min;
Random random = new Random();
int i = random.nextInt(diff + 1) + min;

Класс SecureRandom

В следующем примере формируется массив псевдослучайных значений типа byte :

SecureRandom random = new SecureRandom();
byte bytes[] = new byte;
random.nextBytes(bytes);

Этот же массив можно сформировать методом generateSeed :

 byte seed[] = random.generateSeed(8);

Пример использования SecureRandom представлен на странице
Симметричного шифрования.

Класс ThreadLocalRandom

В JDK 7 включен класс ThreadLocalRandom из многопоточного пакета
java.util.concurrent, который следует использовать для получения псевдослучайных
значений в многопоточных приложениях. Для получения экземпляра ThreadLocalRandom следует использовать
статический метод current() данного класса. Пример :

ThreadLocalRandom random = ThreadLocalRandom.current();

System.out.println("Random values : ");
System.out.println("boolean : " + random.nextBoolean());
System.out.println("int : "     + random.nextInt    ());
System.out.println("float : "   + random.nextFloat  ());
System.out.println("long : "    + random.nextLong   ());

System.out.println("int from 0 to 5 : "   + 
                                  random.nextInt(5));
System.out.println("long from 5 to 15 : " + 
                                  random.nextLong(5, 15));