Python matrix

NumPy N-мерный массив

NumPy — это библиотека Python, которая может использоваться для научных и числовых приложений, а также инструмент для операций с линейной алгеброй.

Основной структурой данных в NumPy является ndarray, который является сокращенным именем для N-мерного массива. При работе с NumPy данные в ndarray просто называются массивом.

Это массив фиксированного размера в памяти, который содержит данные одного типа, такие как целые числа или значения с плавающей запятой.

Доступ к типу данных, поддерживаемому массивом, можно получить через атрибут «dtype» в массиве. Доступ к измерениям массива можно получить через атрибут «shape», который возвращает кортеж, описывающий длину каждого измерения. Есть множество других атрибутов. Узнайте больше здесь:

N-мерный массив

Простой способ создать массив из данных или простых структур данных Python, таких как список, — это использовать функцию array ().

В приведенном ниже примере создается список Python из трех значений с плавающей запятой, затем создается ndarray из списка и осуществляется доступ к форме и типу массивов.

При выполнении примера печатается содержимое ndarray, фигура, которая является одномерным массивом с 3 элементами, и тип данных, который является 64-битной плавающей точкой.

Slicing arrays

Slicing in python means taking elements from one given index to another given
index.

We pass slice instead of index like this: .

We can also define the step, like this: .

If we don’t pass start its considered 0

If we don’t pass end its considered length of array in that dimension

If we don’t pass step its considered 1

Example

Slice elements from index 1 to index 5 from the following array:

import numpy as nparr = np.array()print(arr)

Note: The result includes the start index, but excludes the end index.

Example

Slice elements from index 4 to the end of the array:

import numpy as nparr = np.array()print(arr)

Example

Slice elements from the beginning to index 4 (not included):

import numpy as nparr = np.array()print(arr)

1.4.1.6. Copies and views¶

A slicing operation creates a view on the original array, which is
just a way of accessing array data. Thus the original array is not
copied in memory. You can use to check if two arrays
share the same memory block. Note however, that this uses heuristics and may
give you false positives.

When modifying the view, the original array is modified as well:

>>> a = np.arange(10)
>>> a
array()
>>> b = a)
>>> np.may_share_memory(a, b)
True
>>> b = 12
>>> b
array()
>>> a   # (!)
array()

>>> a = np.arange(10)
>>> c = a)

>>> np.may_share_memory(a, c)
False

This behavior can be surprising at first sight… but it allows to save both
memory and time.

8.1. Создание индексных массивов

Преобразует срез в столбец, а последовательности соединяет вдоль второй оси.

Преобразует срез в строку, а последовательности соединяет вдоль первой оси

Создает объект среза.

Возвращает индексы ненулевых элементов массива.

Возвращает элементы, которые могут выбираться из двух массивов в зависимости от условия.

Возвращает координатную сетку для пространства заданной размерности и заданного размера.

Возвращает открытую координатную сетку созданную из одномерных массивов.

Возвращает открытую координатную сетку значений.

Преобразует кортеж массивов индексов в плоский массив индексов.

Преобразует плоский массив индексов в кортеж массивов индексов.

Возвращает индексы элементов главной диагонали квадратного массива заданного размера и размерности.

Возвращает индексы элементов главной диагонали указанного массива.

Индексы элементов квадратного массива выбранные по некоторому условию (маске массива).

Возвращает индексы элементов нижнего треугольника массива указанного размера.

Возвращает индексы элементов нижнего треугольника указанного массива.

Возвращает индексы элементов верхнего треугольника массива указанного размера.

Возвращает индексы элементов верхнего треугольника указанного массива.

Объединение массивов

NumPy предоставляет множество функций для создания новых массивов из существующих массивов.

Давайте рассмотрим две наиболее популярные функции, которые вам могут понадобиться или с которыми вы столкнетесь.

Вертикальный стек

Имея два или более существующих массива, вы можете сложить их вертикально, используя функцию vstack ().

Например, учитывая два одномерных массива, вы можете создать новый двумерный массив с двумя строками, сложив их вертикально.

Это продемонстрировано в примере ниже.

Выполнение примера сначала печатает два отдельно определенных одномерных массива. Массивы вертикально сложены, что приводит к новому массиву 2 × 3, содержимое и форма которого печатаются.

Горизонтальный стек

Имея два или более существующих массива, вы можете разместить их горизонтально, используя функцию hstack ().

Например, учитывая два одномерных массива, вы можете создать новый одномерный массив или одну строку со сцепленными столбцами первого и второго массивов.

Это продемонстрировано в примере ниже.

Выполнение примера сначала печатает два отдельно определенных одномерных массива. Затем массивы располагаются горизонтально, что приводит к созданию нового одномерного массива с 6 элементами, содержимое и форма которого печатаются

Python NumPy

NumPy IntroNumPy Getting StartedNumPy Creating ArraysNumPy Array IndexingNumPy Array SlicingNumPy Data TypesNumPy Copy vs ViewNumPy Array ShapeNumPy Array ReshapeNumPy Array IteratingNumPy Array JoinNumPy Array SplitNumPy Array SearchNumPy Array SortNumPy Array FilterNumPy Random
Random Intro
Data Distribution
Random Permutation
Seaborn Module
Normal Distribution
Binomial Distribution
Poisson Distribution
Uniform Distribution
Logistic Distribution
Multinomial Distribution
Exponential Distribution
Chi Square Distribution
Rayleigh Distribution
Pareto Distribution
Zipf Distribution

NumPy ufunc
ufunc Intro
ufunc Create Function
ufunc Simple Arithmetic
ufunc Rounding Decimals
ufunc Logs
ufunc Summations
ufunc Products
ufunc Differences
ufunc Finding LCM
ufunc Finding GCD
ufunc Trigonometric
ufunc Hyperbolic
ufunc Set Operations

8.2. Индексоподобные операции

Возвращает элементы массива с указанными индексами вдоль указанной оси.

Сопоставляет одномерные массивы индексов с соответствующими полными срезами исходного массива вдоль указанной оси и возвращает найденные элементы.

Создает массив на основе индексного массива из набора массивов.

Возвращает указанные срезы массива вдоль заданной оси.

Извлекает диагональ из массива, а так же позволяет строить диагональные массивы.

Возвращает указанные диагонали массива.

Возвращает массив составленный из элементовдругих массивов, которые выбираются из них в зависимости от указанного условия.

Возвращает представление массива с указанной формой и смещением байтов между элементами для перехода по ним вдоль разных осей.

Случайные величины (numpy.random)¶

В модуле numpy.random собраны функции для генерации массивов случайных чисел различных распределений и свойств.
Их можно применять для математического моделирования. Функция random() создает массивы из псевдослучайных чисел,
равномерно распределенных в интервале (0, 1). Функция RandomArray.randint() для получения массива равномерно
распределенных чисел из заданного интервала и заданной формы. Можно получать и случайные перестановки с помощью
RandomArray.permutation(). Доступны и другие распределения для получения массива нормально распределенных величин
с заданным средним и стандартным отклонением:

Следующая таблица приводит основные функции модуля.

Команда	Описание
rand(d0, d1, …, dn)	набор случайных чисел заданной формы
randn()	набор (или наборы) случайных чисел со стандартным нормальным распределением
randint(low)	случайные целые числа от low (включая) до high (не включая).
random_integers(low)	случайные целые числа между low и high (включая).
random_sample()	случайные рациональные числа из интервала [0.0, 1.0).
bytes(length)	случайные байты
shuffle(x)	тасовка элементов последовательностина месте
permutation(x)	возвращает последовательность, переставленных случайным образом элементов
seed()	перезапуск генератора случайных чисел
beta(a, b)	числа с Бетта- распределением \(f(x,\alpha,\beta)=\frac{1}{B(\alpha,\beta)}x^{\alpha-1}(1-x)^{\beta-1}\) \(B(\alpha,\beta)=\int_0^1 t^{\alpha-1}(1-t)^{\beta-1}dt\)
binomial(n, p)	числа с биномиальным распределением \(P(N)= \left( \frac{n}{N} \right) p^N (1-p)^{n-N}\)
chisquare(df)	числа с распределением хи-квадрат \(p(x)=\frac{(1/2)^{k/2}}{\Gamma(k/2)} x^{k/2-1} e^{-x/2}\)
mtrand.dirichlet(alpha)	числа с распределением Дирихле (alpha – массив параметров).
exponential()	числа с экспоненциальным распределением \(f(x,\frac{1}{\beta})=\frac{1}{\beta}exp(-\frac{x}{\beta})\)
f(dfnum, dfden)	числа с F распределением (dfnum – число степеней свободы числителя > 0; dfden –число степеней свободы знаменателя >0.)
gamma(shape)	числа с Гамма — распределением
geometric(p)	числа с геометрическим распределением
gumbel()	числа с распределением Гумбеля
hypergeometric(ngood, nbad, nsample)	числа с гипергеометрическим распределением (n = ngood, m = nbad, and N = number of samples)
laplace()	числа с распределением Лапласа
logistic()	числа с логистическим распределением
lognormal()	числа с логарифмическим нормальным распределением
logseries(p)	числа с распределением логарифмического ряда
multinomial(n, pvals)	числа с мультиномиальным распределением
multivariate_normal(mean, cov)	числа с мульти нормальным распределением (mean – одномерный массив средних значений; cov – двухмерный симметричный, полож. определенный массив (N, N) ковариаций
negative_binomial(n, p)	числа с отрицательным биномиальным распределением
noncentral_chisquare(df, nonc)	числа с нецентральным распределением хи-квадрат
noncentral_f(dfnum, dfden, nonc)	числа с нецентральным F распределением (dfnum — целое > 1; dfden – целое > 1; nonc : действительное >= 0)
normal()	числа с нормальным распределением
pareto(a)	числа с распределением Паретто
poisson()	числа с распределением Пуассона
power(a)	числа со степенным распределением
rayleigh()	числа с распределением Релея
standard_cauchy()	числа со стандартным распределением Коши
standard_exponential()	числа со стандартным экспоненциальным распределением
standard_gamma(shape)	числа с гамма- распределением
standard_normal()	числа со стандартным нормальным распределением (среднее=0, сигма=1).
standard_t(df)	числа со стандартным распределением Стьюдента с df степенями свободы
triangular(left, mode, right)	числа из треугольного распределения
uniform()	числа с равномерным распределением
vonmises(mu, kappa)	числа с распределением Майсеса (I- модифицированная функция Бесселя)
wald(mean, scale)	числа с распределением Вальда
weibull(a)	числа с распределением Вайбулла
zipf(a)	числа с распределением Зипфа (зетта функция Римана)

3.8. Арифметические операции

Поэлементно вычисляет наименьшее общее кратное массивов x1 и x2.

Поэлементно вычисляет наибольший общий делитель массивов x1 и x2.

Поэлементная сумма значений массивов.

Вычисляет обратное значение () каждого элемента массива.

Эквивалентно простому копированию () элементов массива, но только для массивов поддерживающих математические операции. Формально соответствует математической записи .

Отрицательное значение элементов массива.

Поэлементное умножение значений массива x1 на значения массива x2.

Поэлементное деление значений массива x1 на значения массива x2.

Поэлементное возведение значений массива x1 в степень равную значениям из массива x2.

Поэлементная разность значений массива x1 и x2.

Поэлементное истинное деление значений массива x1 на значения массива x2.

Поэлементное целочисленное деление значений массива x1 на значения массива x2.

Поэлементное возведение значений массива x1 в степень равную значениям из массива x2, адаптированное для чисел с плавающей точкой.

Поэлементный остаток от деления значений массива x1 на значения массива x2.

Поэлементно вычисляет остаток от деления значений массива x1 на значения массива x2.

Дробная и целая часть элементов массива.

Элементарный остаток от деления значений массива x1 на значения массива x2.

Результат истинного деления и остаток от деления значений массива x1 на значения массива x2.

Access 3-D Arrays

To access elements from 3-D arrays we can use comma separated integers representing
the dimensions and the index of the element.

Example

Access the third element of the second array of the first array:

import numpy as nparr = np.array(, ], , ]])
print(arr)

Example Explained

prints the value .

And this is why:

The first number represents the first dimension, which contains two arrays:
, ]
and:
, ]
Since we selected , we are left with the first array:
, ]

The second number represents the second dimension, which also contains two arrays:

and:

Since we selected , we are left with the second array:

The third number represents the third dimension, which contains three values:
4
5
6
Since we selected , we end up with the third value:
6

Примеры работы с NumPy

Подытожим все вышесказанное. Вот несколько примеров полезных инструментов NumPy, которые могут значительно облегчить процесс написания кода.

Математические формулы NumPy

Необходимость внедрения математических формул, которые будут работать с матрицами и векторами, является главной причиной использования NumPy. Именно поэтому NumPy пользуется большой популярностью среди представителей науки. В качестве примера рассмотрим формулу , которая является центральной для контролируемых моделей машинного обучения, что решают проблемы регрессии:

Реализовать данную формулу в NumPy довольно легко:

Главное достоинство NumPy в том, что его не заботит, если и содержат одно или тысячи значение (до тех пор, пока они оба одного размера). Рассмотрим пример, последовательно изучив четыре операции в следующей строке кода:

У обоих векторов и по три значения. Это значит, что в данном случае равно трем. После выполнения указанного выше вычитания мы получим значения, которые будут выглядеть следующим образом:

Затем мы можем возвести значения вектора в квадрат:

Теперь мы вычисляем эти значения:

Таким образом мы получаем значение ошибки некого прогноза и за качество модели.

Представление данных NumPy

Задумайтесь о всех тех типах данных, которыми вам понадобится оперировать, создавая различные модели работы (электронные таблицы, изображения, аудио и так далее). Очень многие типы могут быть представлены как n-мерные массивы:

Транспонирование и изменение формы матриц в numpy

Нередки случаи, когда нужно повернуть матрицу. Это может потребоваться при вычислении скалярного произведения двух матриц. Тогда возникает необходимость наличия совпадающих размерностей. У массивов NumPy есть полезное свойство под названием , что отвечает за транспонирование матрицы.

Некоторые более сложные ситуации требуют возможности переключения между размерностями рассматриваемой матрицы. Это типично для приложений с машинным обучением, где некая модель может запросить определенную форму вывода, которая является отличной от формы начального набора данных. В таких ситуациях пригодится метод из NumPy. Здесь от вас требуется только передать новые размерности для матрицы. Для размерности вы можете передать , и NumPy выведет ее верное значение, опираясь на данные рассматриваемой матрицы:

Еще больше размерностей NumPy

NumPy может произвести все вышеперечисленные операции для любого количества размерностей. Структура данных, расположенных центрально, называется , или n-мерным массивом.

В большинстве случаев для указания новой размерности требуется просто добавить запятую к параметрам функции NumPy:

Shell

array(,
,
],

,
,
],

,
,
],

,
,
]])

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

array(1.,1., 1.,1., 1.,1., 1.,1., 1.,1., 1.,1., 1.,1., 1.,1., 1.,1., 1.,1., 1.,1., 1.,1.)

Как создаются матрицы в Python?

Добавление и модификация массивов или матриц (matrix) в Python осуществляется с помощью библиотеки NumPy. Вы можете создать таким образом и одномерный, и двумерный, и многомерный массив. Библиотека обладает широким набором пакетов, которые необходимы, чтобы успешно решать различные математические задачи. Она не только поддерживает создание двумерных и многомерных массивов, но обеспечивает работу однородных многомерных матриц.

Чтобы получить доступ и начать использовать функции данного пакета, его импортируют:

import numpy as np

Функция array() — один из самых простых способов, позволяющих динамически задать одно- и двумерный массив в Python. Она создаёт объект типа ndarray:

array = np.array(/* множество элементов */)

Для проверки используется функция array.type() — принимает в качестве аргумента имя массива, который был создан.

Если хотите сделать переопределение типа массива, используйте на стадии создания dtype=np.complex:

array2 = np.array([ /*элементы*/, dtype=np.complex)

Когда стоит задача задать одномерный или двумерный массив определённой длины в Python, и его значения на данном этапе неизвестны, происходит его заполнение нулями функцией zeros(). Кроме того, можно получить матрицу из единиц через функцию ones(). При этом в качестве аргументов принимают число элементов и число вложенных массивов внутри:

np.zeros(2, 2, 2) 

К примеру, так в Python происходит задание двух массивов внутри, которые по длине имеют два элемента:

array(] 
]] 
) 

Если хотите вывести одно- либо двумерный массив на экран, вам поможет функция print(). Учтите, что если матрица слишком велика для печати, NumPy скроет центральную часть и выведет лишь крайние значения. Дабы увидеть массив полностью, используется функция set_printoptions(). При этом по умолчанию выводятся не все элементы, а происходит вывод только первой тысячи. И это значение массива указывается в качестве аргумента с ключевым словом threshold.

Линейная алгебра (numpy.linalg)¶

Модуль numpy.linalg содержит алгоритмы линейной алгебры, в частности нахождение определителя матрицы, решений
системы линейных уравнений, обращение матрицы, нахождение собственных чисел и собственных векторов матрицы,
разложение матрицы на множители: Холецкого, сингулярное, метод наименьших квадратов и т.д.

Команда	Описание
dot(a, b)	скалярное произведение массивов
vdot(a, b)	векторное произведение векторов
inner(a, b)	внутреннее произведение массивов
outer(a, b)	внешнее произведение векторов
tensordot(a, b)	тензорное скалярное произведение вдоль оси (размерность больше 1)
einsum(subscripts, *operands)	суммирование Эйншнейна Evaluates the Einstein summation convention on the operands.
linalg.matrix_power(M, n)	возведение квадратной матрицы в степень n
kron(a, b)	произведение Кронекера двух массивов
linalg.norm(a)	норма матрицы или вектора.
linalg.cond(a)	число обусловленности матрицы.
linalg.det(a)	определитель
linalg.slogdet(a)	знак и натуральный логарифм определителя
trace(a)	сумма элементов по диагонали.
linalg.cholesky(a)	разложение Холецкого
linalg.qr(a)	разложение QR
linalg.svd(a)	сингулярное разложение
linalg.solve(a, b)	решение линейного матричного уравнения или системы скалярных уравнений.
linalg.tensorsolve(a, b)	решение тензорного уравнения a x = b для x.
linalg.lstsq(a, b)	решение матричного уравнения методом наименьших квадратов
linalg.inv(a)	обратная матрица (для умножения)
linalg.pinv(a)	псевдо-обратная матрица (Мура-Пенроуза)
linalg.tensorinv(a)	«обратный» к многомерному массиву
linalg.eig(a)	собственные значения и правые собственные вектора квадратной
linalg.eigh(a)	собственные значения и собственные вектора эрмитовой или симметричной матрицы
linalg.eigvals(a)	собственные значения произвольной матрицы
linalg.eigvalsh(a)	собственные значения эрмитовой или действительной симметричной матрицы

1.4.1.3. Basic data types¶

You may have noticed that, in some instances, array elements are displayed with
a trailing dot (e.g. vs ). This is due to a difference in the
data-type used:

>>> a = np.array()
>>> a.dtype
dtype('int64')

>>> b = np.array()
>>> b.dtype
dtype('float64')

Tip

Different data-types allow us to store data more compactly in memory,
but most of the time we simply work with floating point numbers.
Note that, in the example above, NumPy auto-detects the data-type
from the input.

You can explicitly specify which data-type you want:

>>> c = np.array(, dtype=float)
>>> c.dtype
dtype('float64')

The default data type is floating point:

>>> a = np.ones((3, 3))
>>> a.dtype
dtype('float64')

There are also other types:

Перестройка массива

После нарезки данных вам может понадобиться изменить их.

Например, некоторые библиотеки, такие как scikit-learn, могут требовать, чтобы одномерный массив выходных переменных (y) был сформирован как двумерный массив с одним столбцом и результатами для каждого столбца.

Некоторые алгоритмы, такие как рекуррентная нейронная сеть с короткой кратковременной памятью в Keras, требуют ввода данных в виде трехмерного массива, состоящего из выборок, временных шагов и функций.

Важно знать, как изменить ваши массивы NumPy, чтобы ваши данные соответствовали ожиданиям конкретных библиотек Python. Мы рассмотрим эти два примера

Форма данных

Массивы NumPy имеют атрибут shape, который возвращает кортеж длины каждого измерения массива.

Например:

При выполнении примера печатается кортеж для одного измерения.

Кортеж с двумя длинами возвращается для двумерного массива.

Выполнение примера возвращает кортеж с количеством строк и столбцов.

Вы можете использовать размер измерений вашего массива в измерении формы, например, указав параметры.

К элементам кортежа можно обращаться точно так же, как к массиву, с 0-м индексом для числа строк и 1-м индексом для количества столбцов. Например:

Запуск примера позволяет получить доступ к конкретному размеру каждого измерения.

Изменить форму 1D в 2D Array

Обычно требуется преобразовать одномерный массив в двумерный массив с одним столбцом и несколькими массивами.

NumPy предоставляет функцию reshape () для объекта массива NumPy, который можно использовать для изменения формы данных.

Функция reshape () принимает единственный аргумент, который задает новую форму массива. В случае преобразования одномерного массива в двумерный массив с одним столбцом кортеж будет иметь форму массива в качестве первого измерения (data.shape ) и 1 для второго измерения.

Собрав все это вместе, мы получим следующий проработанный пример.

При выполнении примера печатается форма одномерного массива, изменяется массив, чтобы иметь 5 строк с 1 столбцом, а затем печатается эта новая форма.

Изменить форму 2D в 3D Array

Обычно требуется преобразовать двумерные данные, где каждая строка представляет последовательность в трехмерный массив для алгоритмов, которые ожидают множество выборок за один или несколько временных шагов и одну или несколько функций.

Хорошим примером являетсямодель в библиотеке глубокого обучения Keras.

Функция изменения формы может использоваться напрямую, указывая новую размерность. Это ясно с примером, где каждая последовательность имеет несколько временных шагов с одним наблюдением (функцией) на каждый временной шаг.

Мы можем использовать размеры в атрибуте shape в массиве, чтобы указать количество выборок (строк) и столбцов (временных шагов) и зафиксировать количество объектов в 1

Собрав все это вместе, мы получим следующий проработанный пример.

При выполнении примера сначала печатается размер каждого измерения в двумерном массиве, изменяется форма массива, а затем суммируется форма нового трехмерного массива.

Статистика¶

Команда	Описание
amin(a)	минимум в массиве или минимумы вдоль одной из осей
amax(a)	максимум в массиве или максимумы вдоль одной из осей
nanmax(a)	максимум в массиве или максимумы вдоль одной из осей (игнорируются NaN).
nanmin(a)	минимум в массиве или минимумы вдоль одной из осей (игнорируются NaN).
ptp(a)	диапазон значений (максимум — минимум) вдоль оси
average(a)	взвешенное среднее вдоль оси
mean(a)	арифметическое среднее вдоль оси
median(a)	вычисление медианы вдоль оси
std(a)	стандартное отклонение вдоль оси
corrcoef(x)	коэффициенты корреляции
correlate(a, v)	кросс-корреляция двух одномерных последовательностей
cov(m)	ковариационная матрица для данных
histogram(a)	гистограмма из набора данных
histogram2d(x, y)	двумерная гистограмма для двух наборов данных
histogramdd(sample)	многомерная гистограмма для данных
bincount(x)	число появление значения в массиве неотрицательных значений
digitize(x, bins)	возвращает индексы интервалов к которым принадлежат элементы массива

Арифметические операции над массивами NumPy

Создадим два массива NumPy и продемонстрируем выгоду их использования.

Массивы будут называться и :

При сложении массивов складываются значения каждого ряда. Это сделать очень просто, достаточно написать :

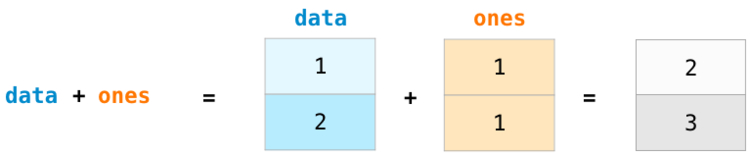
Новичкам может прийтись по душе тот факт, что использование абстракций подобного рода не требует написания циклов for с вычислениями. Это отличная абстракция, которая позволяет оценить поставленную задачу на более высоком уровне.

Помимо сложения, здесь также можно выполнить следующие простые арифметические операции:

Довольно часто требуется выполнить какую-то арифметическую операцию между массивом и простым числом. Ее также можно назвать операцией между вектором и скалярной величиной. К примеру, предположим, в массиве указано расстояние в милях, и его нужно перевести в километры. Для этого нужно выполнить операцию :

Как можно увидеть в примере выше, NumPy сам понял, что умножить на указанное число нужно каждый элемент массива. Данный концепт называется трансляцией, или broadcating. Трансляция бывает весьма полезна.

Python NumPy

NumPy IntroNumPy Getting StartedNumPy Creating ArraysNumPy Array IndexingNumPy Array SlicingNumPy Data TypesNumPy Copy vs ViewNumPy Array ShapeNumPy Array ReshapeNumPy Array IteratingNumPy Array JoinNumPy Array SplitNumPy Array SearchNumPy Array SortNumPy Array FilterNumPy Random
Random Intro
Data Distribution
Random Permutation
Seaborn Module
Normal Distribution
Binomial Distribution
Poisson Distribution
Uniform Distribution
Logistic Distribution
Multinomial Distribution
Exponential Distribution
Chi Square Distribution
Rayleigh Distribution
Pareto Distribution
Zipf Distribution

NumPy ufunc
ufunc Intro
ufunc Create Function
ufunc Simple Arithmetic
ufunc Rounding Decimals
ufunc Logs
ufunc Summations
ufunc Products
ufunc Differences
ufunc Finding LCM
ufunc Finding GCD
ufunc Trigonometric
ufunc Hyperbolic
ufunc Set Operations

Prerequisites¶

Before reading this tutorial you should know a bit of Python. If you
would like to refresh your memory, take a look at the Python
tutorial.

If you wish to work the examples in this tutorial, you must also have
some software installed on your computer. Please see
https://scipy.org/install.html for instructions.

Learner profile

This tutorial is intended as a quick overview of
algebra and arrays in NumPy and want to understand how n-dimensional
() arrays are represented and can be manipulated. In particular, if
you don’t know how to apply common functions to n-dimensional arrays (without
using for-loops), or if you want to understand axis and shape properties for
n-dimensional arrays, this tutorial might be of help.

Learning Objectives

After this tutorial, you should be able to:

Транспонирование матрицы

Транспонирование матрицы в основном включает в себя переворачивание матрицы по соответствующим диагоналям, т. е. Меняет местами строки и столбцы входной матрицы. Строки становятся столбцами и наоборот.

Например: давайте рассмотрим матрицу A с размерами 3 × 2, т.е. 3 строки и 2 столбца. После выполнения операции транспонирования размеры матрицы A будут 2 × 3, т.е. 2 строки и 3 столбца.

основном выполняет транспонирование входной матрицы и создает новую в результате операции транспонирования.

Пример:

import numpy
 
matA = numpy.array()
print("Original Matrix A:\n")
print(matA)
print('\nDimensions of the original MatrixA: ',matA.shape)
print("\nTranspose of Matrix A:\n ")
res = matA.T
print(res)
print('\nDimensions of the Matrix A after performing the Transpose Operation:  ',res.shape)

Выход:

Original Matrix A:


 ]

Dimensions of the original MatrixA: (2, 5)

Transpose of Matrix A:
 

 
 
 
 ]

Dimensions of the Matrix A after performing the Transpose Operation: (5, 2)

В приведенном выше фрагменте кода я создал матрицу размером 2 × 5, т.е. 2 строки и 5 столбцов.

После выполнения операции транспонирования размеры результирующей матрицы составляют 5 × 2, то есть 5 строк и 2 столбца.

7.4. Генерация случайных значений

Очень многие вычислительные методы требуют генерации случайных значений. В некоторых ситуациях, на генерируемые данные накладываются очень строгие и высокие требования. NumPy содержит функции для генерации простых случайных данных, функции генерации случайных перестановок, а так же большое количество функций для гернерации случайных чисел с всевозможными вероятностными распределениями.

Получение простых случайных данных:

Перестановки:

NumPy предоставляет порядка 30 функций, позволяющих генерировать случайные числа с самыми разными вероятностными распределениями:

Вы так же имеете доступ к состоянию генератора случайных чисел, а так же можете управлять им:

Copies and Views¶

When operating and manipulating arrays, their data is sometimes copied
into a new array and sometimes not. This is often a source of confusion
for beginners. There are three cases:

No Copy at All

Simple assignments make no copy of objects or their data.

>>> a = np.array(,
...                4,  5,  6,  7],
...                8,  9, 10, 11]])
>>> b = a            # no new object is created
>>> b is a           # a and b are two names for the same ndarray object
True

Python passes mutable objects as references, so function calls make no
copy.

>>> def f(x):
...     print(id(x))
...
>>> id(a)                           # id is a unique identifier of an object
148293216  # may vary
>>> f(a)
148293216  # may vary

View or Shallow Copy

Different array objects can share the same data. The method
creates a new array object that looks at the same data.

>>> c = a.view()
>>> c is a
False
>>> c.base is a                        # c is a view of the data owned by a
True
>>> c.flags.owndata
False
>>>
>>> c = c.reshape((2, 6))                      # a's shape doesn't change
>>> a.shape
(3, 4)
>>> c, 4 = 1234                      # a's data changes
>>> a
array(,
       ,
       ])

Slicing an array returns a view of it:

>>> s = a  , 13     # spaces added for clarity; could also be written "s = a"
>>> s = 10           # s is a view of s. Note the difference between s = 10 and s = 10
>>> a
array(,
       ,
       ])

Deep Copy

The method makes a complete copy of the array and its data.

>>> d = a.copy()                          # a new array object with new data is created
>>> d is a
False
>>> d.base is a                           # d doesn't share anything with a
False
>>> d, = 9999
>>> a
array(,
       ,
       ])

Sometimes should be called after slicing if the original array is not required anymore.
For example, suppose is a huge intermediate result and the final result only contains
a small fraction of , a deep copy should be made when constructing with slicing:

>>> a = np.arange(int(1e8))
>>> b = a[:100.copy()
>>> del a  # the memory of ``a`` can be released.

If is used instead, is referenced by and will persist in memory
even if is executed.