Основные модули python

Экспоненциальные и логарифмические функции

import cmath
a = 3 + 4j
print('e^c =', cmath.exp(a))
print('log2(c) =', cmath.log(a, 2))
print('log10(c) =', cmath.log10(a))
print('sqrt(c) =', cmath.sqrt(a))

Вывод:

e^c = (-13.128783081462158-15.200784463067954j)
log2(c) = (2.321928094887362+1.3378042124509761j)
log10(c) = (0.6989700043360187+0.4027191962733731j)
sqrt(c) = (2+1j)

Другие

Есть несколько разных функций, чтобы проверить, является ли комплексное число конечным, бесконечным или . Также есть функция проверки близости двух комплексных чисел.

>>> print(cmath.isfinite(2 + 2j))
True

>>> print(cmath.isfinite(cmath.inf + 2j))
False

>>> print(cmath.isinf(2 + 2j))
False

>>> print(cmath.isinf(cmath.inf + 2j))
True

>>> print(cmath.isinf(cmath.nan + 2j))
False

>>> print(cmath.isnan(2 + 2j))
False

>>> print(cmath.isnan(cmath.inf + 2j))
False

>>> print(cmath.isnan(cmath.nan + 2j))
True

>>> print(cmath.isclose(2+2j, 2.01+1.9j, rel_tol=0.05))
True

>>> print(cmath.isclose(2+2j, 2.01+1.9j, abs_tol=0.005))
False

Графический интерфейс

В стандартной библиотеке Python есть
графическая библиотека интерфейсов
Tkinter. Но при помощи внешних модулей вы
можете поднять GUI ваших приложений на
новый уровень.

wxPython. Создает по-настоящему нативные пользовательские интерфейсы для Python-приложений, которые могут запускаться на Windows, Mac и Linux, а также прочих Unix-подобных системах практически без каких-либо модификаций.

PyGObject. Пакет Python, предоставляющий привязки для библиотек на базе Gobject, таких как GTK, GStreamer, WebKitGTK, GLib, GIO и др.

Pmw. Набор инструментов для создания на Python высокоуровневых составных виджетов (с использованием модуля Tkinter).

WCK. Расширение API, позволяющее реализовывать на чистом Python всевозможные пользовательские виджеты.

Tix. Мощный набор компонентов пользовательского интерфейса, при помощи которого можно расширить возможности ваших Tcl/Tk и Python-приложений. Использование Tix вместе с Tk очень улучшает внешний вид и функционал приложений.

Python Tutorial

Python HOMEPython IntroPython Get StartedPython SyntaxPython CommentsPython Variables
Python Variables
Variable Names
Assign Multiple Values
Output Variables
Global Variables
Variable Exercises

Python Data TypesPython NumbersPython CastingPython Strings
Python Strings
Slicing Strings
Modify Strings
Concatenate Strings
Format Strings
Escape Characters
String Methods
String Exercises

Python BooleansPython OperatorsPython Lists
Python Lists
Access List Items
Change List Items
Add List Items
Remove List Items
Loop Lists
List Comprehension
Sort Lists
Copy Lists
Join Lists
List Methods
List Exercises

Python Tuples
Python Tuples
Access Tuples
Update Tuples
Unpack Tuples
Loop Tuples
Join Tuples
Tuple Methods
Tuple Exercises

Python Sets
Python Sets
Access Set Items
Add Set Items
Remove Set Items
Loop Sets
Join Sets
Set Methods
Set Exercises

Python Dictionaries
Python Dictionaries
Access Items
Change Items
Add Items
Remove Items
Loop Dictionaries
Copy Dictionaries
Nested Dictionaries
Dictionary Methods
Dictionary Exercise

Python If…ElsePython While LoopsPython For LoopsPython FunctionsPython LambdaPython ArraysPython Classes/ObjectsPython InheritancePython IteratorsPython ScopePython ModulesPython DatesPython MathPython JSONPython RegExPython PIPPython Try…ExceptPython User InputPython String Formatting

Гиперболические функции

Подобно тригонометрическим функциям, гиперболические функции для комплексного числа также доступны в модуле .

import cmath

a = 3 + 4j

print('Hyperbolic Sine:', cmath.sinh(a))
print('Hyperbolic Cosine:', cmath.cosh(a))
print('Hyperbolic Tangent:', cmath.tanh(a))

print('Inverse Hyperbolic Sine:', cmath.asinh(a))
print('Inverse Hyperbolic Cosine:', cmath.acosh(a))
print('Inverse Hyperbolic Tangent:', cmath.atanh(a))

Вывод:

Hyperbolic Sine: (-6.5481200409110025-7.61923172032141j)
Hyperbolic Cosine: (-6.580663040551157-7.581552742746545j)
Hyperbolic Tangent: (1.000709536067233+0.00490825806749606j)
Inverse Hyperbolic Sine: (2.2999140408792695+0.9176168533514787j)
Inverse Hyperbolic Cosine: (2.305509031243477+0.9368124611557198j)
Inverse Hyperbolic Tangent: (0.11750090731143388+1.4099210495965755j)

cmath vs math

A complex number is a combination of a real number and an imaginary number. It has the formula of a + bi, where a is the real number and bi is the imaginary number. Real and imaginary numbers can be explained as follows:

• A real number is literally any number you can think of.
• An imaginary number is a number that gives a negative result when squared.

A real number can be any number. For example, 12, 4.3, -19.0 are all real numbers. Imaginary numbers are shown as i. The following image shows an example of a complex number:

In the example above, 7 is the real number and 3i is the imaginary number. Complex numbers are mostly used in geometry, calculus, scientific calculations, and especially in electronics.

The functions of the Python module aren’t equipped to handle complex numbers. However, Python provides a different module that can specifically deal with complex numbers, the module. The Python module is complemented by the module, which implements many of the same functions but for complex numbers.

You can import the module as follows:

>>>

Since the module is also packaged with Python, you can import it the same way you imported the module. Before you work with the module, you have to know how to define a complex number. You can define a complex number as follows:

>>>

As you can see, you can determine that a number is indeed complex by using .

Note: In mathematics, the imaginary unit is usually denoted i. In some fields, it’s more customary to use j for the same thing. In Python, you use to denote imaginary numbers.

Python also provides a special built-in function called that lets you create complex numbers. You can use as follows:

>>>

You can use either method to create complex numbers. You can also use the module to calculate mathematical functions for complex numbers as follows:

>>>

Практическая работа. Создание собственного модуля

Программист на Python всегда может создать собственный модуль, чтобы использовать его в нескольких своих программах или даже предоставить в пользование всему миру. В качестве тренировки создадим модуль с функциями для вычисления площадей прямоугольника, треугольника и круга:

from math import pi, pow

def rectangle(a, b):
    return round(a * b, 2)

def triangle(a, h):
    return round(0.5 * a * h, 2)

def circle(r):
    return round(pi * pow(r, 2), 2) 

Здесь также иллюстрируется принцип, что один модуль может импортировать другие. В данном случае импортируются функции из модуля math.

Поместите данный код в отдельный файл square.py. Однако куда поместить сам файл?

Когда интерпретатор Питона встречает команду импорта, то просматривает на наличие файла-модуля определенные каталоги. Их перечень можно увидеть по содержимому sys.path:

>>> import sys
>>> sys.path
['', '/usr/lib/python35.zip', '/usr/lib/python3.5', 
'/usr/lib/python3.5/plat-x86_64-linux-gnu',
'/usr/lib/python3.5/lib-dynload', 
'/home/pl/.local/lib/python3.5/site-packages',
'/usr/local/lib/python3.5/dist-packages', 
'/usr/lib/python3/dist-packages']

Это список адресов в Linux. В Windows он будет несколько другим. Первый элемент – пустая строка, что обозначает текущий каталог, то есть то место, где сохранена сама программа, импортирующая модуль. Если вы сохраните файл-модуль и файл-программу в одном каталоге, то интерпретатор без труда найдет модуль.

Также модуль можно положить в любой другой из указанных в списке каталогов. Тогда он будет доступен для всех программ на Python, а также его можно будет импортировать в интерактивном режиме.

Можно добавить в sys.path свой каталог. Однако в этом случае либо код программы должен содержать команды изменения значения sys.path, либо надо править конфигурационный файл операционной системы. В большинстве случаев лучше так не делать.

Поместите файл square.py в тот же каталог, где будет исполняемая программа. Ее код должен включать инструкцию импорта модуля square (при импорте расширение файла не указывается) и вызов той функции и с теми параметрами, которые ввел пользователь. Т. е. у пользователя надо спросить, площадь какой фигуры он хочет вычислить. Далее запросить у него аргументы для соответствующей функции. Передать их в функцию из модуля square, а полученный оттуда результат вывести на экран.

Примечание. Исполнение модуля как самостоятельного скрипта, а также создание строк документации, которые отображает встроенная в Python функция help(), будут рассмотрены в курсе объектно-ориентированного программирования.

Импорт модуля

Если запустить в каталоге, в котором лежит данный модуль (например, my_module.py), интерпретатор:

>>> python

и потом сделать импорт модуля:

>>> import my_module

то мы получаем доступ ко всем функциям, которые в модуле определены:

>>> my_module.func1()
>>> my_module.func2()
...

Для более короткой записи можно создать локальную переменную:

>>> f1 = my_module.func1

Второй вариант импорта — взятие непосредственно имени без имени модуля:

>>> from my_module import func1, func2
>>> func1()

Третий вариант импорта — включение всех имен, определенных в модуле:

>>> from my_module import *
>>> func1()

Для предотвращения конфликта имен можно использовать создание алиаса:

>>> from my_module import open as my_open

Пример. Импорт на основе from обладает такой особенностью, что он делает импортируемые атрибуты read-only:

>>> from small import x, y
>>> x = 42

В данном случае x — это локальная переменная, в то время как переменные x, y в самом модуле small не меняются:

>>> import small
>>> small.x = 42

здесь x — глобальная переменная.

Во избежание недоразумений import предпочтительнее без from в тех случаях, когда один и тот же модуль используется в нескольких местах.

Поскольку модуль загружается один раз, для его повторной загрузки можно использовать функцию reload().

Каждый модуль имеет собственное пространство имен, являющееся глобальной областью видимости для всех определенных в нем функций. Для того чтобы переменные этого модуля не попали в конфликт с другими глобальными именами или другими модулями, нужно использовать префикс: _имя_модуля_._имя_переменной_ .

Модули могут импортировать другие модули. Обычно инструкцию import располагают в начале модуля или программы.

Операции с числами

Является ли переменная числом

Любую переменную можно проверить на тип (int, float или complex):

Если вы хотите проверить, находится ли в строке число, воспользуйтесь методом

Однако стоит помнить, что метод не работает для отрицательных чисел и чисел с плавающей точкой.

Также для проверки на число, можно написать собственную функцию:

Арифметические операции

• – сложение;
• – вычитание;
• – умножение;
• – деление;
• – целочисленное деление;
• – остаток от деления;
• – возведение в степень;
• – смена знака;
• – модуль числа;
• – возвращает кортеж из частного и остатка от деления x на y;
• – возведение числа в степень (z – деление по модулю);
• – округление числа (ndigits — знаки после запятой).

Преобразования

• – преобразование в целое число
• – преобразование в число с плавающей точкой
• – преобразование в комплексное число
• – целоe числа в двоичную строку;
• – целое число в восьмеричную строку;
• – целое число в шестнадцатеричную строку;
• – перевод целого числа 123 в список цифр этого числа;
• – перевод списка цифр в целое число 123;
• – число в строку;

Ввод чисел

Для ввода данных в программу на языке Python используется функция . Эта функция считывает то что вы ввели на клавиатуре, и записывает эти данные в переменную в виде одной строки. После этого, перевести строку в число можно простыми функциями , или

Если нужен список чисел, введите несколько чисел через пробел и выполните:

Вывод чисел

Для вывода числа используйте

На практике возникают ситуации, когда нужно вывести число вместе со строкой (например пояснить, что означает число). Существует несколько вариантов сделать это:

Другие полезные функции

• – посчитает длину числа;
• – если остаток от деления равен 0, то число четное;
• – диапазон чисел от 0 до 5, по которому можно итерироваться;
• – перевернет число (123 -> 321).

Звук

Благодаря нескольким очень полезным
модулям работать со звуком в Python довольно
просто.

pySonic. Python-враппер для высокопроизводительной кроссплатформенной звуковой библиотеки FMOD.

PyMedia. Модуль Python для манипуляций с файлами WAV, MP3, Ogg, AVI, DivX, DVD, CD-DA и др. Позволяет анализировать, демультиплексировать и мультиплексировать, декодировать и кодировать все поддерживаемые форматы. Может компилироваться для Windows, Linux и Cygwin.

PMIDI. Библиотека PMIDI служит оберткой для библиотеки Windows MIDI Streams, обеспечивая возможность использования последней в Python. Благодаря PMIDI разработчики могут на лету генерировать в своем коде синтезированные музыкальные последовательности, чтобы они проигрывались для пользователей.

Mutagen. Модуль для обработки метаданных аудио. Поддерживает аудиофайлы FLAC, M4A, Musepack, MP3, Ogg FLAC, Ogg Speex, Ogg Theora, Ogg Vorbis, True Audio и WavPack.

Библиотека Statsmodel в Python

С помощью пакета Statsmodel можно выполнять статистические вычисления, которые включают в себя описательную статистику, логический вывод, а также оценку для различных статистических моделей. Это способствует эффективному статистическому исследованию данных.

Ниже приведен пример реализации библиотеки Statsmodel в Python.

Python

import numpy as np
import statsmodels.api as sm
import statsmodels.formula.api as smf

input_data = sm.datasets.get_rdataset(«Guerry», «HistData»).data

res = smf.ols(‘Lottery ~ Literacy + np.log(Pop1831)’, data = input_data).fit()
print(res.summary())

1 2 3 4 5 6 7 8 9

importnumpy asnp importstatsmodels.api assm importstatsmodels.formula.api assmf input_data=sm.datasets.get_rdataset(«Guerry»,»HistData»).data res=smf.ols(‘Lottery ~ Literacy + np.log(Pop1831)’,data=input_data).fit() print(res.summary())

Манипуляции с изображениями и видео

Python это очень мощный язык; с его помощью
можно решать многие задачи, например,
работать с изображениями. Стандартная
библиотека не имеет встроенного
функционала для этих целей, но следующие
модули вам помогут.

Python Imaging Library (PIL). PIL добавляет в интерпретатор Python возможность обработки изображений. Эта библиотека поддерживает много форматов файлов и предоставляет хороший функционал для работы с графикой.

Gdmodule. Это интерфейс для библиотеки GD, созданной Томасом Баутелом.

VideoCapture. Win32-расширение для доступа к таким видеоустройствам, как веб-камеры (USB) и ТВ-карты.

MoviePy. Библиотека Python для редактирования видео: обрезка, склейка, вставка надписей, нелинейное редактирование, обработка видео и создание пользовательских эффектов.

pyscreenshot. Кроссплатформенный модуль, позволяющий делать скриншоты без установки сторонних библиотек.

Логические операции с десятичным модулем

Decimal содержит набор встроенных функций для выполнения логических операций с десятичными числами, таких как AND, OR, XOR и т. Д.

• Функция logical_and(): выполняет операцию логического И над двумя десятичными числами и возвращает результат.
• Функция logical_or(): выполняет операцию логического ИЛИ над двумя десятичными числами и возвращает результат.
• Функция logical_xor(): выполняет логическую операцию XOR над двумя десятичными числами и возвращает результат.

#Syntax for logical_and() function-
decimal1.logical_and(decimal2)

#Syntax for logical_or() function-
decimal1.logical_or(decimal2)

#Syntax for logical_xor() function-
decimal1.logical_xor(decimal2)

Пример:

import decimal as d

valx = d.Decimal(1001)
valy = d.Decimal(1111)

print("Value 1: ",valx)
print("Value 2: ",valy)

AND = valx.logical_and(valy)
print("The logical AND value of the two decimals: ",AND)

OR = valx.logical_or(valy)
print("The logical OR value of the two decimals: ",OR)

XOR = valx.logical_xor(valy)
print("The logical XOR value of the two decimals: ",XOR)

Выход:

Value 1:  1001
Value 2:  1111
The logical AND value of the two decimals:  1001
The logical OR value of the two decimals:  1111
The logical XOR value of the two decimals:  110

7.1.1. Значения -inf, inf и nan

Возможно вы обратили внимание на то, что когда мы вычисляли натуральный логарифм массива, среди значений которого был ноль, не появилось абсолютно никакой ошибки, а сам логарифм стал равен значению (минус бесконечность). Убедимся в этом еще раз:. Более того, в NumPy мы даже можем делить на ноль:

Более того, в NumPy мы даже можем делить на ноль:

NumPy предупредил нас о том, что встретил деление на ноль, но тем не менее выдал ответ (плюс бесконечность). Дело в том, что с математической точки зрения все абсолютно верно — если вы что-то делите на бесконечно малое значение то в результате получете значение, которое окажется бесконечно большим. Если результатом математической операции является плюс или минус бесконечность, то логичнее выдать значение или чем выдавать ошибку.

В NumPy есть еще одно специальное значение — . Данное значение выдается тогда, когда результат вычислений не удается определить:

Заметьте, что NumPy нас просто предупредил о том, что ему попалось недопустимое значение, но ошибки не возникло. Дело в том, что в реальных вычислениях значения , или встречается очень часто, поэтому появление этого значения проще обрабатывать специальными методами (функции и ), чем постоянно лицезреть сообщения об ошибках.

Новичкам, довольно трудно привыкнуть, к тому что в недрах компьютера вся арифметика на самом деле является двоичной и с этим связано очень много казусов. Во первых не совсем понятно, когда ждать появления значений и :

Число 1.633123935319537e+16 появилось потому что в NumPy выполняются арифметические, а не символьные вычисления, т. е. число π хранится в памяти компьютера не как знание о том, что это математическая константа с бесконечным количеством десятичных знаков после запятой, а как обычное число с десятичной точкой (десятичная дробь) равная числу π с очень маленькой, но все же, погрешностью:

NumPy отличает предельные случаи, когда вычисления выполнить невозможно, например, деление на ноль. В таких случаях появляются значения , и . Если из-за самых незначительных погрешностей вычисления все же возможны, то NumPy их обязательно выполнит. В этих случаях вместо значений или у вас будут появляться самые маленькие или самые большие числа, которые возможно представить на вашем компьютере.

Тем не менее и на этом сюрпризы не заканчиваются. Если число 1.633123935319537e+16 является самым больши, которое может появиться при вычислениях, оно вполне ожидаемо должно появиться в самых разных ситуациях. Например:

То, есть какая-то, длинная арифметика все же доступна — очень хорошая новость, для лбителей криптографии и теории чисел. Но иногда:

В заключение могу лишь сказать, что все предельные случаи требуют кардинальных решений. Некоторые решения имеются в самом NumPy, некоторые предоставляют другие пакеты. Если вам необходимы точные решения, то лучше обратиться к системам компьютерной алгебры и символьных вычислений, например пакету SymPy — маленький, но мощьный пакет Python для символьных вычислений. Если вы решили отправиться в самые дебри теории чисел, алгебры и криптографии, то лучшим решением окажется программа GAP. Программа GAP не является программой Python, но имеет Python интерфейс в замечательной программе Sage, которая определенно заслуживает вашего внмания.

math[править]

Модуль math всегда доступен и обеспечивает доступ к математическим функциям.

Данные функции неприменимы к комплексным числам, для работы с комплексными числами имеются функции с теми же именами в модуле cmath.

Модуль содержит следующие функции. Во всех случаях, кроме особо оговоренных, функции возвращают число типа float.

Теоретико-численные функции и функции представленияправить

• math.ceil

  Возвращает округленное x как ближайшее целое значение типа float, большее или равное x (округление «вверх»).

  (x)

• math.copysign

  Возвращает число x со знаком числа y. На платформе, поддерживающей знак нуля copysign(1.0, -0.0) даст -1.0.

  (x, y)

• math.fabs

  Возвращает абсолютное значение (модуль) числа x. В Python есть встроенная функция abs, но она возвращает модуль числа с тем же типом, что число, здесь же всегда float abs (fabs).

  (x)

• math.factorial

  Возвращает факториал целого числа x, если x не целое возбуждается ошибка ValueError.

  (x)

• math.floor

  В противоположность ceil(x) возвращает округленное x как ближайшее целое значение типа float, меньшее или равное x (округление «вниз»).

  (x)

• math.fmod

  Аналогична функции fmod(x, y) библиотеки C. Отметим, что это не то же самое, что выражение Python x%y. Желательно использовать при работе с объектами float, в то время как x % y больше подходит для int.

  (x, y)

• math.frexp

  Представляет число в экспоненциальной записи x=m∗2e{\displaystyle x=m*2^{e}} и возвращает мантиссу m (действительное число, модуль которого лежит в интервале от 0.5 до 1) и порядок e (целое число) как пару чисел (m, e). Если x=0, то возвращает (0.0, 0)

  (x)

• math.fsum

  Возвращает float сумму от числовых элементов итерируемого объекта.

  (iterable)

• math.isinf

  Проверяет, является ли float объект x плюс или минус бесконечностью, результат соответственно True или False.

  (x)

• math.isnan

  Проверяет, является ли float объект x объектом NaN (not a number).

  (x)

• math.ldexp

  Возвращает значение x∗2i{\displaystyle x*2^{i}}, то есть осуществляет действие, обратное функции math.frexp(x).

  (x, i)

• math.modf

  Возвращает часть, идущую после запятой и целую часть от float числа. Оба результата сохраняют знак исходного числа x и представлены типом float.

  (x)

• math.trunc

  Возвращает целую часть числа x в виде int объекта.

  (x)

Степенные и логарифмические функцииправить

• math.exp

  Возвращает ex{\displaystyle e^{x}}.

  (x)

• math.log

  При передаче функции одного аргумента x, возвращает натуральный логарифм x. При передаче двух аргументов, второй берется как основание логарифма.

  (x)

• math.log1p

  Возвращает натуральный логарифм от x+1.

  (x)

• math.log10

  Возвращает десятичный логарифм x.

  (x)

• math.pow

  Возвращает xy{\displaystyle x^{y}}.

  (x, y)

• math.sqrt

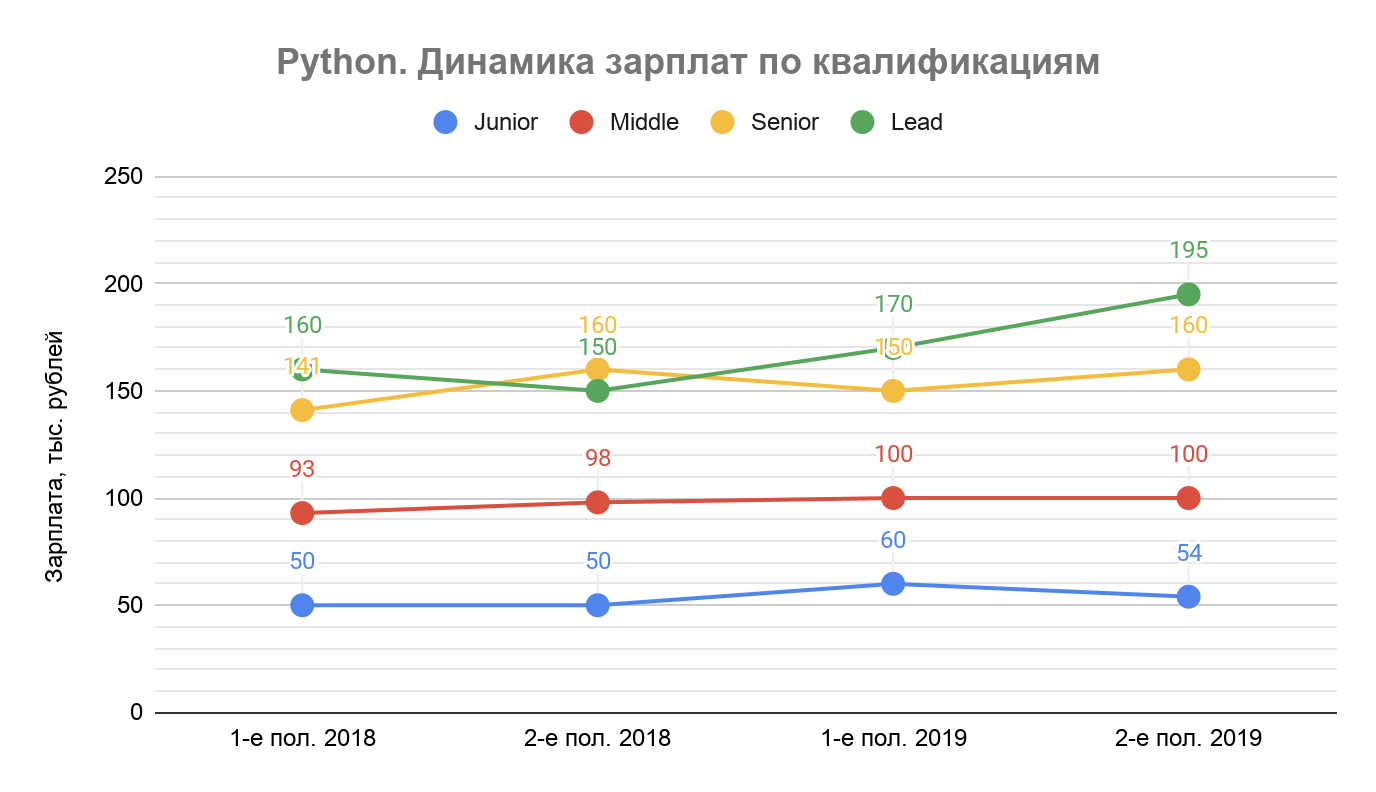
  Квадратный корень (square root) из x.

  (x)

Тригонометрические функцииправить

• math.acos

  Возвращает арккосинус x, в радианах.

  (x)

• math.asin

  Возвращает арксинус x, в радианах.

  (x)

• math.atan

  Возвращает арктангенс x, в радианах.

  (x)

• math.atan2

  Возвращает atan(y/x), в радианах. Результат лежит в интервале . Вектор, конец, которого задается точкой (x, y) образует угол с положительным направлением оси x. Поэтому эта функция имеет более общее назначение, чем предыдущая. Например и atan(1), и atan2(1, 1) дадут в результате pi/4, но atan2(-1, -1) это уже -3*pi/4.

  (y, x)

• math.cos

  Возвращает косинус x, где x выражен в радианах.

  (x)

• math.hyp

  Возвращает евклидову норму, то есть sqrt(x**2+y**2). Удобно для вычисления гипотенузы (hyp) и длины вектора.

  (x, y)

• math.sin

  Возвращает синус x, где x выражен в радианах.

  (x)

• math.tan

  Возвращает тангенс x, где x выражен в радианах.

  (x)

Радианы в градусы и наоборотправить

• math.degrees

  Конвертирует значение угла x из радиан в градусы.

  (x)

• math.radians

  Конвертирует значение угла x из градусов в радианы.

  (x)

Гиперболические функцииправить

Смысл ясен из названий и соответствует стандартным обозначениям англоязычной литературы:

• math.acosh(x)
• math.asinh(x)
• math.atanh(x)
• math.cosh(x)
• math.sinh(x)
• math.tanh(x)

Веб-разработка

Python это популярный язык для веб-разработки.
Все пакеты Python, перечисленные в этом
разделе, делают жизнь веб-разработчика
гораздо проще.

Beautiful Soup. Библиотека Python для быстрого парсинга HTML- и XML-файлов.

scrape. Модуль Python для веб-браузинга и скрапинга.

mechanize. Очень полезный модуль, благодаря которому вы получаете эмулятор браузера для взаимодействия с веб-страницами.

libgmail. Обеспечивает доступ к гугловскому сервису Gmail.

Google Maps. Благодаря этому модулю можно использовать веб-сервисы платформы Google Maps в своем приложении на Python.

Requests позволяет невероятно легко отсылать HTTP/1.1-запросы.

Selenium. При помощи этого модуля разработчики могут программными методами открывать веб-страницы, заполнять поля, кликать по кнопкам и отсылать формы.

pyquery позволяет делать jQuery-запросы в XML-документах. API этой библиотеки максимально приближен к jQuery. Для быстрой манипуляции с XML и HTML pyquery использует LXML.