Традиционные шифры

Масонский шифр

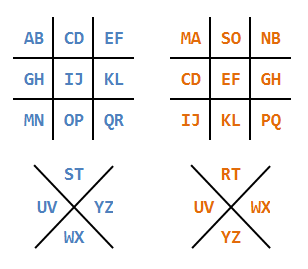
Масонский шифр известен также под названием «пигпен» (Pigpen) или «крестики-нолики». Этот шифр представляет собой простой шифр замены, в котором каждой букве алфавита соответствует графический символ, вычисляемой по одной из приведённых ниже сеток.

Чтобы зашифровать определённую букву при помощи этого шифра, нужно сначала определить место, где эта буква находится в одной из четырёх сеток, а затем нарисовать ту часть сетки, которая окружает эту букву. То есть, как-то так:

Если знать ключ (то, как буквы расположены в сетках), то разгадать такую надпись довольно легко. А вот если буквы в сетках изначально расставлены по какому-то неизвестному правилу (с ключевым словом, поочерёдно или вообще случайно), то в этой ситуации всегда может помочь

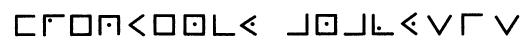
Использование графических символов вместо букв не является большим препятствием для криптоанализа, и эта система идентична другим простым схемам моноалфавитного замещения. Благодаря своей простоте, данный шифр часто упоминается в детских книжках про шифрование, тайнопись и всякие другие шпионские штучки.

Точное время происхождения шифра неизвестно, но некоторые из найденных записей этой системы датируются XVIII веком. Вариации этого шифра были использованы орденом розенкрейцеров и масонами. Последние использовали его в своих тайных документах и переписках довольно часто, поэтому шифр и стали называть шифром масонов. Даже на надгробиях масонов можно увидеть надписи, использующие данный шифр. Похожая система шифрования использовалась во время гражданской войны в США армией Джорджа Вашингтона, а также заключенными в федеральных тюрьмах Конфедераций Штатов США.

Ниже приведены два (синий и красный) варианта заполнения сетки таких шифров. Буквы расположены парами, вторая буква из пары рисуется символом с точкой:

Пример работы

Если мы зашиф­ру­ем так фра­зу «При­вет, это жур­нал Код!», то можем полу­чить что-то такое:

hi857ов9njg5jоlр6;p0ора

Шту­ка в том, что одна и та же бук­ва в шиф­ров­ке не озна­ча­ет оди­на­ко­вые бук­вы в исход­ном сооб­ще­нии, пото­му что биты шиф­ро­ва­ния выбра­ны слу­чай­ным обра­зом. Поэто­му при попыт­ке рас­шиф­ров­ки зло­умыш­лен­ник полу­чит такие варианты:

Сроч­но под­пи­шись на код

Вер­ни день­ги, а то вилы

мама, я сдал зачёт, ура

Ваш зам пре­да­тель и вор

Ваш зам ни при чём, вот

Так­же он может полу­чить любые дру­гие соче­та­ния букв, цифр и про­бе­лов в рам­ках тех 23 сим­во­лов, кото­рые у нас были в исход­ном сооб­ще­нии. Может быть, это не текст вовсе, а набор цифр. Может быть, это текст на каком-то дру­гом язы­ке. Может быть, это не текст вовсе, а очень малень­кая кар­тин­ка. Все эти вари­ан­ты мож­но полу­чить из нашей зашиф­ро­ван­ной стро­ки, пото­му что зло­умыш­лен­ник не зна­ет ключ. 

Авторские шифры

Шифров, где одному символу алфавита (букве, цифре, знаку препинания) соответствует один (реже больше) графический знак, придумано великое множество. Большинство из них придуманы для использования в фантастических фильмах, мультфильмах и компьютерных играх. Вот некоторые из них:

Пляшущие человечки

Один из самых известных авторских шифров подстановки – это «Пляшущие человечки». Его придумал и описал английский писатель Артур Конан Дойл в одном из своих произведений про Шерлока Холмса. Буквы алфавита заменяются символами, похожими на человечков в разных позах. В книге человечки были придуманы не для всех букв алфавита, поэтому фанаты творчески доработали и переработали символы, и получился вот такой шифр:

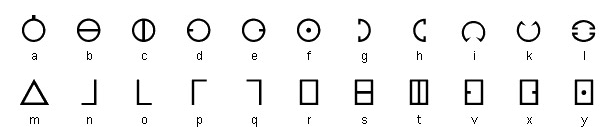
А вот такой алфавит описал в своём трактате «Утопия» Томас Мор в 1516 году:

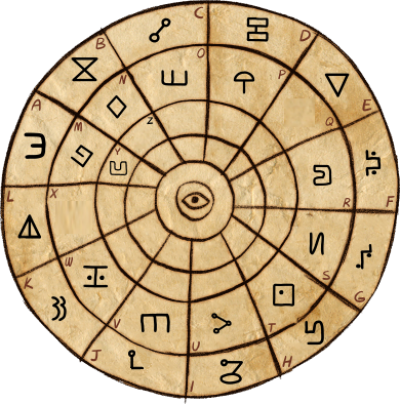
Стэнфорда Пайнса (автора дневников)

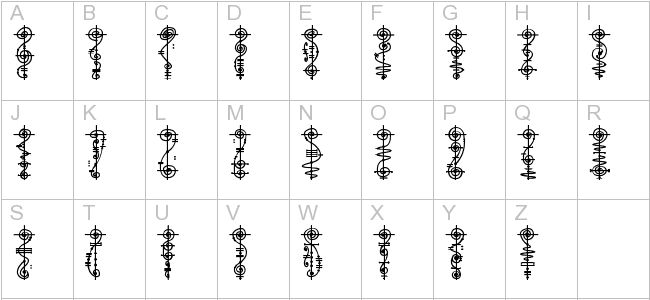
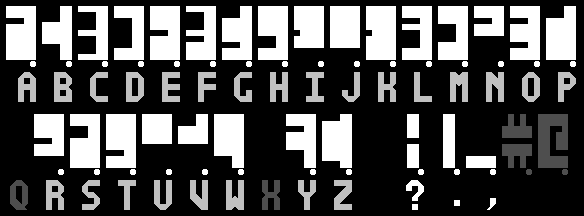
Al Bhed

Это только малая толика подобных шифров-алфавитов. Также можно почитать более подробно про шифры замены (подстановки), про перестановочные и комбинированные шифры.

Как работает шифрование на примере iMessage?

Пожалуй, именно Apple можно отнести к категории тех компаний, которые максимально беспокоятся о конфиденциальности данных своих пользователей. Шифрование и защита в продуктах Apple находится на высоком уровне.

Понять это можно, разобравшись в принципах работы одного из сервисов — iMessage.

Итак, вы решили использовать iMessage. Зарегистрировали Apple ID, зашли в настройки и включили сервис.

На iOS-девайсе тут же создаются две пары ключей: публичная и приватная. Да-да, iMessage работает по ассиметричному типу шифрования.

Приватная пара остается в памяти устройства, публичная же отправляется на сервера Apple.

Ну что, iMessage включен. Вы открываете приложение «Сообщения», выбираете адресата и начинаете писать сообщение. Тем временем сервис проверяет наличие публичного ключа адресата, который прикреплен к учетной записи Apple ID. Найдя его, абонент подсвечивается доступным для отправки сообщений через сервис.

Сообщение написано, вы нажимаете Отправить. Сообщение тут же копируется и проходит процедуру шифрования с помощью хранящегося на девайсе приватного ключа, подвязывается к публичному ключу и отправляется адресату.

Зашифрованное сообщение поступает на устройство получателя. Оно привязано к публичному ключу отправителя и требует дешифровки. Тем временем на сервере удаляется та самая зашифрованная копия.

Несмотря на то, что пользователь уже «физически» получил сообщение, он об этом не знает, поскольку никаких уведомлений не получал. Девайс приступает к дешифровке. Включается обратный шифрованию алгоритм. Используя известный публичный ключ и приватный ключ, хранящийся на устройстве, сообщение дешифруется.

Прочесть его без наличия самого устройства невозможно даже в случае перехвата сообщения. Когда расшифровка сообщения окончена, пользователь получает уведомление. А дальше весь процесс повторяется вновь и вновь.

Маршрутная перестановка

Обычное транспонирование таблицы (заполняем по строкам, читаем по столбцам) можно усложнить и считывать не по столбцам, а змейкой, зигзагом, по спирали или каким-то другим способом, т.е. задавать маршрут обхода таблицы. Такие способы заполнения таблицы если и не усиливают стойкость шифра, то делают процесс шифрования гораздо более занимательным. Правда, процесс расшифровки при этом усложняется, особенно, если маршрут неизвестен, и его ещё надо узнать.

На рисунке сверху последовательность символов «АБВГДЕЁЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯ.,?» вписана построчно в таблицу 6×6, а затем считана по маршруту, указанному линиями. Получаются следующие шифровки:

1. АЁЛСЧЭБЖМТШЮВЗНУЩЯГИОФЪ.ДЙПХЫ,ЕКРЦЬ?
2. АЁЛСЧЭЮЯ.,?ЬЦРКЕДГВБЖМТШЩЪЫХПЙИЗНУФО
3. АБЁЛЖВГЗМСЧТНИДЕЙОУШЭЮЩФПКРХЪЯ.ЫЦЬ,?
4. АЁЛСЧЭЮШТМЖБВЗНУЩЯ.ЪФОИГДЙПХЫ,?ЬЦРКЕ
5. НЗВБАЁЖМЛСТШЧЭЮЯЩУФЪ.,?ЬЫХЦРПЙКЕДГИО

А здесь нужно обходить таблицу «ходом коня», причём маршрут уже нарисован, так что это совсем для маленьких 🙂

Но если подать эту головоломку так, как показано ниже, то будет уже совсем не просто, так как вариантов обхода ходом коня может быть много, и нужно будет найти из всех этих вариантов единственный правильный (ниже зашифровано «Пушкин. Медный всадник»).

Ещё один метод загадать маршрут — использовать мнемоническое стихотворение, в котором некими ключевыми словами заданы координаты обхода сетки. Допустим, есть шахматная доска, которую ходом шахматного коня нужно всю обойти клетка за клеткой так, чтобы побывать на каждой клетке только один раз. В результате получится маршрут длиной 64. Один из многих миллионов таких маршрутов показан на картинке ниже. Если в порядке обхода клеток вписать сообщение, то чтобы его разгадать, нужно будет восстановить этот самый маршрут.

А вот загадать этот маршрут можно, например, вот таким стихотворением:

Алеет Осень Ценными Дарами,
Еще Один Животворящий День.
Хлеба Червонят Желтыми Шнурами,
Хрустальных Вод Философична Сень.

Два Вечера Цеплявшиеся Шишки
Артист Писал, Бездонна Синева.
Дорожный Шлак Целуют Червячишки,
Еще Покрыта Флоксами Трава.

Дымится Чай Эффектней Шоколада,
Фарфоры Чашек Достаются Трем,
Блондинке Девушка Дана Отрада
Форшмак Делить Холодным Острием.

Жена, Толкая Хилую Подругу,
Желает Сняться Этим Выходным,
Ценя Сама Арктическую Вьюгу,
Бросает Шар Арбуза Четверым.

Цикад Пяток, Едва Чревовещая,
Дарует Дрему Фикусам Окна.
Хотя Довольны Жаждавшие Чая,
Хозяин Шумно Жертвует Вина.

Фокстротами Шесть Девушек Пленились,
Эстрадных Танцев Фантастичней Па,
Едва Ступающий Цыпленок Вылез,
А Селезень Блуждающий Пропал.

Алеет Тело Бронзовой Осины,
Царит Теней Ажурная Длина.
Беззвучней, Чем Автомобиля Шины,
Болоту Ветер Дарит Семена.

Фонарь Восьмью Химерами Сияет,
Жук Прилетает, Хлопая, Туда.
Желанна Осень, Если Довершает
Ценнейший Отдых Бодрого Труда.

Разгадывать его придётся так: «Алеет Осень» — это А1 (А Один), «Ценными Дарами» — C2 (Цэ Два), «Ещё Один» — E1 (E Один), «Животворящий День» — G2 (Жэ Два) и т.д.

Шифр Вернама — это сложно

Теперь попро­бу­ем объ­яс­нить подробнее. 

1. Сооб­ще­ние хра­нит­ся в виде битов дан­ных. Допу­стим, мы шиф­ру­ем текст. Ком­пью­тер не уме­ет рабо­тать с тек­стом как тако­вым, он этот текст хра­нит как набор чис­ло­вых кодов (про­ще гово­ря, у ком­пью­те­ра все бук­вы про­ну­ме­ро­ва­ны и он пом­нит толь­ко эти номера).

Чис­ла, в свою оче­редь, ком­пью­тер хра­нит в виде дво­ич­но­го кода, то есть битов дан­ных. Это пока что не отно­сит­ся к шиф­ро­ва­нию, это про­сто то, как хра­нит­ся любая тек­сто­вая инфор­ма­ция в компьютере.

Бук­ва	Код в ASCII	Биты дан­ных
K	75	01001011
O	79	01001111
D	68	01000100

Если мы напи­шем KOD в коди­ров­ке ASCII, то для ком­пью­те­ра это будет после­до­ва­тель­ность из трёх чисел, а каж­дое чис­ло — это набор битов: 

01001011 01001111 01000100

2. Берём слу­чай­ные биты в каче­стве клю­ча шиф­ро­ва­ния. На вхо­де у нас три чис­ла по 8 бит. Что­бы их зашиф­ро­вать, нам нуж­ны 24 слу­чай­ных бита. Возь­мём их с потол­ка, они ниче­го не значат: 

10101101 01111010 10101011

3. Накла­ды­ва­ем коды друг на дру­га и при­ме­ня­ем алго­ритм шиф­ро­ва­ния. Шифр Вер­на­ма постро­ен на прин­ци­пе «исклю­ча­ю­ще­го ИЛИ», он же XOR. Он смот­рит на каж­дую пару битов и пыта­ет­ся понять, они оди­на­ко­вые или раз­ные. Если биты оди­на­ко­вые, резуль­тат про­вер­ки будет 0, если раз­ные — 1.

Мож­но про­ве­рить себя так: XOR зада­ёт вопрос «Эти биты раз­ные»? Если да — то 1, если нет — то 0.

Бук­ва K	1	1	1	1
Ключ	1	1	1	1	1
XOR (Они разные?)	1	1	1	1	1

Если мы таким обра­зом зако­ди­ру­ем три бук­вы, мы полу­чим три новых набо­ра битов: 

KOD (сооб­ще­ние)	01001011	01001111	01000100
Ключ	10101101	01111010	10101011
Резуль­тат шиф­ро­ва­ния с помо­щью XOR	11100110	00110101	11101111

Полу­ча­ет­ся, что на вхо­де у нас было 24 бита дан­ных и на выхо­де 24 бита дан­ных. Но эти дан­ные теперь совсем дру­гие. Если пере­ве­сти эти чис­ла обрат­но в текст, мы получим: 

KOD → æ5ï

Boxcryptor

Еще одно впечатляющее программное обеспечение для шифрования ваших файлов, Boxcryptor использует передовое сквозное шифрование для более чем 30 различных облачных провайдеров.

Его внешний вид не один из самых юзер-френдли, но он довольно прост в использовании.

После установки инструмента он автоматически найдет папки облачного хранилища в вашей системе и добавит их в качестве местоположений.

Как только это будет сделано, вам не нужно проделывать множество действий.

Просто перетащите файлы или папки в правильные места, и они будут зашифрованы сами по себе.

Помимо обмена через поставщиков облачных хранилищ, вы также можете обмениваться файлами непосредственно с другим пользователем Boxcryptor.

Это бесплатно для личного использования, если вы используете одного поставщика облачного хранилища.

Чтобы использовать больше и доступ к большему количеству функций, вы можете просто обновить его план, начиная с 48 долларов в год.

Стойкость шрифта

Криптографическая стойкость алгоритма шифрования — это способность противостоять взлому. Данный параметр является самым важным для любого шифрования. Очевидно, что шифр простой замены, расшифровку которого осилит любое электронное устройство, является одним из самых нестойких.

На сегодняшний день не существует единых стандартов, по которым можно было бы оценить стойкость шифра. Это трудоемкий и долгий процесс. Однако есть ряд комиссий, которые изготовили стандарты в этой области. Например, минимальные требования к алгоритму шифрования Advanced Encryption Standart или AES, разработанные в NIST США.

Для справки: самым стойким шифром к взлому признан шифр Вернама. При этом его плюсом является то, что по своему алгоритму он является простейшим шифром.

Перестановка «Волшебный квадрат»

Волшебными (или магическими) квадратами называются квадратные таблицы со вписанными в их клетки последовательными натуральными числами от 1 до n2 (где n — размерность квадрата), которые дают в сумме по каждому столбцу, каждой строке и каждой диагонали одно и то же число.

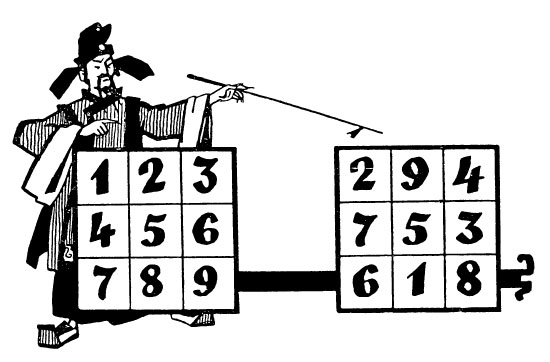
В известном ещё в Древнем Китае квадрате Ло-Шу третьего порядка (3×3) константа квадрата 15 повторяется 8 раз:

• по трём горизонталям: 2+9+4 = 7+5+3 = 6+1+8 = 15
• по трём вертикалям: 2+7+6 = 9+5+1 = 4+3+8 = 15
• по двум диагоналям: 2+5+8 = 4+5+6 = 15

Кстати, константу нечетного квадрата легко посчитать, умножив среднее число ряда, из которого составлен квадрат, на порядок квадрата. Для квадрата 3-го порядка (3×3) константа равна ₁₂₃₄5₆₇₈₉*3=15.

Итак, у нас вначале есть квадрат с числами по порядку, а затем, когда из них составлен «магический» квадрат, цифры идут уже не по порядку. Это и используют при шифровании.

Чтобы зашифровать какое-то послание, нужно сначала подобрать или составить подходящий по размеру волшебный квадрат, затем нарисовать пустую таблицу такого же размера, и вписать буквы текста по очереди в таблицу в соответствии с номерами в волшебном квадрате. Затем выписывают построчно буквы из таблицы в одну длинную строку. Порядок квадрата должен быть равен округлённому в большую сторону корню из длины шифруемой строки, чтобы строка полностью вошла в квадрат. Если строка короче, то остаток можно заполнить произвольными буквами или цифрами.

На первый взгляд кажется, будто магических квадратов очень мало. Тем не менее, их число очень быстро возрастает с увеличением размера квадрата

Так, существует лишь один магический квадрат размером 3х3, если не принимать во внимание его повороты и отражения. Счёт волшебным квадратам 4-го порядка уже идёт на сотни, 5-го — на сотни тысяч

Поэтому магические квадраты больших размеров могли быть хорошей основой для надежной системы шифрования того времени (в Древнем Китае), так как ручной перебор всех вариантов ключа для этого шифра был немыслим.

Есть очень простой метод составления нечётных волшебных квадратов, т.е. размером 3×3, 5×5, 7×7 и т.д. Это метод «террас» или «пирамидок».

Рисуется квадрат нужного размера и к нему пририсовываются ступенчатые «террасы» (обозначены пунктиром). Далее по диагоналям сверху вниз направо квадрат заполняется последовательными числами. После этого «террасы» переносятся внутрь квадрата: правые — налево, левые — направо, верхние — вниз, а нижние — наверх. Получается волшебный квадрат!

На базе этого метода можно составлять разные головоломки. Если использовать метод напрямую, то получится вот такая головоломка:

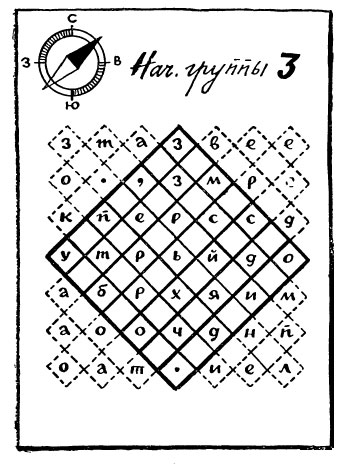
Чтобы решить эту головоломку, нужно буквы из «террас» перенести в квадрат, тогда в квадрате прочитается полное сообщение. Здесь зашифрована фраза «За мостом засада, пройти нельзя, переходите речку в брод.»

А если использовать метод наоборот, то получится головоломка типа такой.

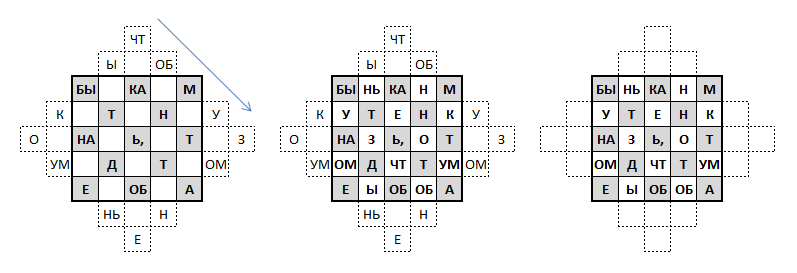
Чтобы её решить, надо вытащить соответствующие буквы из квадрата в «террасы».

Для квадратов 4×4, 6×6 и т.д. таких простых способов их составления не существует, поэтому проще использовать готовые. Например, квадрат Дюрера.

«Энигма»

Всем известно, что «Энигма» — это главная шифровальная машина нацистов во время II мировой войны. Строение «Энигмы» включает комбинацию электрических и механических схем. То, каким получится шифр, зависит от начальной конфигурации «Энигмы». В то же время «Энигма» автоматически меняет свою конфигурацию во время работы, шифруя одно сообщение несколькими способами на всем его протяжении.

В противовес самым простым шифрам «Энигма» давала триллионы возможных комбинаций, что делало взлом зашифрованной информации почти невозможным. В свою очередь, у нацистов на каждый день была заготовлена определенная комбинация, которую они использовали в конкретный день для передачи сообщений. Поэтому даже если «Энигма» попадала в руки противника, она никак не способствовала расшифровке сообщений без введения нужной конфигурации каждый день.

Взломать «Энигму» активно пытались в течение всей военной кампании Гитлера. В Англии в 1936 г. для этого построили один из первых вычислительных аппаратов (машина Тьюринга), ставший прообразом компьютеров в будущем. Его задачей было моделирование работы нескольких десятков «Энигм» одновременно и прогон через них перехваченных сообщений нацистов. Но даже машине Тьюринга лишь иногда удавалось взламывать сообщение.

ROT1 и шифр Цезаря

Название этого шифра ROTate 1 letter forward, и он известен многим школьникам. Он представляет собой шифр простой замены. Его суть заключается в том, что каждая буква шифруется путем смещения по алфавиту на 1 букву вперед. А -> Б, Б -> В, …, Я -> А. Например, зашифруем фразу «наша Настя громко плачет» и получим «общб Обтуа дспнлп рмбшеу».

Шифр ROT1 может быть обобщен на произвольное число смещений, тогда он называется ROTN, где N — это число, на которое следует смещать шифрование букв. В таком виде шифр известен с глубокой древности и носит название «шифр Цезаря».

Шифр Цезаря очень простой и быстрый, но он является шифром простой одинарной перестановки и поэтому легко взламывается. Имея подобный недостаток, он подходит только для детских шалостей.

Зачем изучать старые шифры?

В интернете криптографические протоколы используются практически при каждом запросе. Но как же дело обстояло, когда интернета не было и в помине? Не стоит думать, что в те далекие лохматые времена не было криптографии. Первые способы шифрования появились около четырех тысяч лет назад. Конечно, это были самые примитивные и нестойкие шифры, однако и население тогда было малограмотное, так что такие способы могли защитить информацию от любопытных глаз.

Люди всегда нуждались в секретной переписке, поэтому шифрование не стояло на месте. С раскрытием одних шифров придумывали другие, более стойкие. На смену бумажным шифрам пришли шифровальные машины, которым не было равных среди людей. Даже опытному математику не удавалось взломать шифр, рассчитанный на роторной машине. С появлением первых компьютеров требования к защите информации возросли многократно.

Зачем же нам знакомиться с такими древними и нестойкими шифрами, если можно сразу прочитать про DES и RSA — и вуаля, почти специалист? Изучение первых шифров поможет лучше понять, зачем нужна та или иная операция в современном алгоритме шифрования. Например, шифр перестановки, один из первых примитивных алгоритмов, не был забыт, и перестановка — одна из часто встречающихся операций в современном шифровании. Таким образом, чтобы лучше осознать, откуда на самом деле растут ноги у современных алгоритмов, нужно оглянуться на несколько тысяч лет назад.

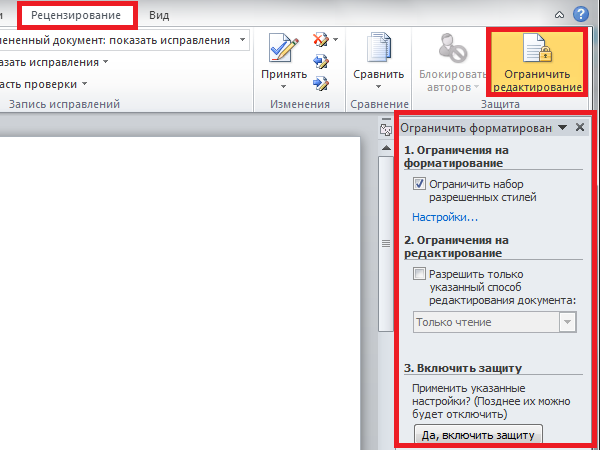
Удаление Пароля открытия из файла Microsoft Word

Существуют три, принципиальных по возможностям удаления пароля, деления версий формата:

• Microsoft Word 6/95 – пароль открытия всегда находится мгновенно
• Microsoft Word 97-2003 (40bit) – пароль искать не целесообразно, проще найти ключ шифрования и расшифровать документ не зная пароля
• Microsoft Word 2007-2016 – пароль открытия ищется только методом перебора, а его скорость можно увеличить за счёт GPU-ускорения на видеокартах AMD/NVIDIA

Пароль на открытие Word 6-95

Это устаревший формат, который встречается всё реже. Для защиты данных в нём применялась примитивная защита, пароль для которой всегда восстанавливается мгновенно, а успех не зависит ни от длины, ни от сложности самого пароля.

Рис. 1: Для взлома Пароля на открытие Word 6-95 достаточно паролеломалки начального уровня

Пароль на открытие Word 97-2003 (40-bit)

Пожалуй, наиболее распространённый на сегодня формат со своими недостатками в защите данных.

Для шифрования в нём используется очень короткий ключ. Это позволяет искать не пароль, а этот самый ключ и гарантирует 100%-ый успех в расшифровке данных. Ведь количество вариантов ключа не меняется вне зависимости от сложности и длины оригинального пароля — оно всегда равно 240 (40 бит, вы помните, да?), а сколько при этом придётся проверить паролей не известно…

Количество вариантов для проверки считается по формуле: число символов в степени длины пароля. То есть (для английского алфавита) это по 26 строчных и заглавных букв, 10 цифр, 8 спецсимволов — в сумме 70 символов. И тогда для 7-ми символьного пароля вариантов будет уже в семь раз больше, чем вариантов ключа шифрования: 707 = 8235430000000 / 240 = 1099511627776

И это без гарантии успеха. А что если длина пароля, скажем, 9 символов?..

Рис.3: Поиск ключа шифрования не требует никаких настроек — выберите файл, запустите поиск

Вся эта история с лёгкостью и 100% гарантией успеха расшифровки 40-ка битных Word 97-2003 (к слову и Excel тоже!) не была бы полной, без упоминания радужных таблиц.

Радужные таблицы содержат заранее просчитанные цепочки ключей шифрования, что в разы сокращает поиск нужного ключа практически без снижения процента успеха. На основе радужных таблиц существуют и онлайн-сервисы для открытия зашифрованных Word файлов.

Рис.4: Радужные таблицы Пасковери в работе на ВерниДоступ.ру

Пароль на открытие Word 2007-2016

Формат набирает популярность и вместе с этим заканчивается время быстрой расшифровки Word файлов. Пароли приходится восстанавливать, то есть попросту перебирать варианты один за другим в надежде, что нужный пароль попадётся в их числе за разумное время.

Помимо увеличения длины ключа шифрования (например, в Word 2013 он уже 256 бит и такой ключ найти нереально), разработчики усложняют и алгоритмы хэширования, замедляя время формирования ключа. При вводе правильного пароля это не заметно, но при переборе миллионов вариантов, падение скорости от версии к версии формата только растёт. Даже в высоко-оптимизированных программах. Даже с GPU ускорением на видеокартах.

Условия успешного поиска «Пароля на открытие» для Word 2007-2016:

манипулирование диапазоном проверки. Умение отсечь лишние проверки позволяет здорово сэкономить время при переборе вариантов. Для манипулирования используют атаку с мутациями по словарям, атаку по простой и позиционной маске. Мутация словарей помогает охватить варианты намеренного изменения пароля из обычного слова, а позиционная маска задать возможные значения для каждой позиции в пароле

GPU ускорение на видеокартах NVIDIA/AMD. Задача поиска пароля отлично масштабируется и способна выполнятся на современных видеокартах. Чем более производительные видеокарты подключаются к поиску, тем выше скорость поиска и тем быстрее может быть достигнут успех

программы для восстановления паролей, заточенные на скорость поиска. Оптимизация в таких программах способна увеличивать скорость перебора вариантов в десятки раз

Поэтому уделяйте особое внимание оценке возможностей программы-паролеломалки по скорости перебора паролей

Типы шифров

История криптографии началась тысячи лет назад. Криптография использует множество различных типов шифрования. Ранние алгоритмы выполнялись вручную и существенно отличаются от современных алгоритмов , которые обычно выполняются машиной.

Исторические шифры

Исторические ручные и бумажные шифры, использовавшиеся в прошлом, иногда называют классическими шифрами . Они включают:

• Замещающий шифр : единицы открытого текста заменяются зашифрованным текстом (например, шифр Цезаря и одноразовый блокнот )
  • Полиалфавитный шифр замещения : шифр замещения, использующий несколько алфавитов замещения (например, шифр Виженера и машину Enigma )
  • Полиграфический шифр замещения : единица замещения представляет собой последовательность из двух или более букв, а не только одну (например, шифр Playfair ).
• Шифр транспонирования : шифротекст представляет собой перестановку открытого текста (например, шифр ограждения рельсов )

Исторические шифры обычно не используются в качестве отдельного метода шифрования, потому что их довольно легко взломать. Многие из классических шифров, за исключением одноразового блокнота, могут быть взломаны с использованием грубой силы .

Современные шифры

Современные шифры более безопасны, чем классические шифры, и предназначены для защиты от широкого спектра атак. Злоумышленник не должен быть в состоянии найти ключ, используемый в современном шифре, даже если он знает какое-либо количество открытого текста и соответствующего зашифрованного текста. Современные методы шифрования можно разделить на следующие категории:

• Частный ключ криптография ( алгоритм симметричного ключа ): тот же ключ используется для шифрования и дешифрования
• Криптография с открытым ключом ( алгоритм асимметричного ключа ): для шифрования и дешифрования используются два разных ключа.

В алгоритме с симметричным ключом (например, DES и AES ) отправитель и получатель должны иметь общий ключ, установленный заранее и хранящийся в секрете от всех других сторон; отправитель использует этот ключ для шифрования, а получатель использует тот же ключ для дешифрования. В алгоритме с асимметричным ключом (например, RSA ) есть два отдельных ключа: открытый ключ публикуется и позволяет любому отправителю выполнять шифрование, в то время как закрытый ключ хранится получателем в секрете и позволяет только ему выполнять правильное дешифрование.

Шифры с симметричным ключом можно разделить на блочные шифры и потоковые шифры . Блочные шифры работают с группами битов фиксированной длины, называемыми блоками, с неизменным преобразованием. Потоковые шифры шифруют цифры открытого текста по одной в непрерывном потоке данных, и преобразование последовательных цифр меняется в процессе шифрования.

Зачем мне знания о криптографии?

Предположим, криптография очень нужна, но пусть ей займутся дядьки с усами математики. Зачем же мне знания по криптографии?

Если ты обычный пользователь — то как минимум, чтобы обеспечить свою приватность. Сегодня крупным государствам и влиятельным организациям становятся доступны средства тотального надзора за миллионами людей. Поэтому криптография оказывается важнейшим инструментом, обеспечивающим конфиденциальность, доверие, целостность, авторизацию сообщений и электронных платежей. Повсеместное распространение криптографии останется одним из немногих способов защитить пользователя от угроз, нависающих над его конфиденциальной информацией. Зная, как работает тот или иной протокол или шифр, чем он хорош и где его слабые места, ты сможешь оcознанно выбирать инструменты для работы или просто общения в Сети.

Короче говоря, криптография используется гораздо чаще, чем можно себе представить. Поэтому пора снять завесу тайны с этой науки, познакомиться с наиболее интересными аспектами и использовать ее возможности себе на пользу.

«Энигма»

Всем известно, что «Энигма» — это главная шифровальная машина нацистов во время II мировой войны. Строение «Энигмы» включает комбинацию электрических и механических схем. То, каким получится шифр, зависит от начальной конфигурации «Энигмы». В то же время «Энигма» автоматически меняет свою конфигурацию во время работы, шифруя одно сообщение несколькими способами на всем его протяжении.

В противовес самым простым шифрам «Энигма» давала триллионы возможных комбинаций, что делало взлом зашифрованной информации почти невозможным. В свою очередь, у нацистов на каждый день была заготовлена определенная комбинация, которую они использовали в конкретный день для передачи сообщений. Поэтому даже если «Энигма» попадала в руки противника, она никак не способствовала расшифровке сообщений без введения нужной конфигурации каждый день.

Взломать «Энигму» активно пытались в течение всей военной кампании Гитлера. В Англии в 1936 г. для этого построили один из первых вычислительных аппаратов (машина Тьюринга), ставший прообразом компьютеров в будущем. Его задачей было моделирование работы нескольких десятков «Энигм» одновременно и прогон через них перехваченных сообщений нацистов. Но даже машине Тьюринга лишь иногда удавалось взламывать сообщение.

Выводы

Опыт истории криптографии показывает нам значимость выбора секретного ключа и частоты смены ключа. Ошибки в этом тяжелом процессе превращают любую систему шифрования в менее стойкую, чем она могла бы быть. В следующий раз поговорим про распределение ключей.

ссылки:

Это первый урок из цикла «Погружение в крипту». Все уроки цикла в хронологическом порядке:

• Уроки криптографии. Основные шифры. часть 1. Основы, исторические шифраторы, как работают (и анализируются) шифры сдвига, замены, Рихарда Зорге, шифр Вернама и шифровальные машины (ты здесь)
• Распределение ключей. часть 2. Что это такое, как выполняется распределение ключей и как выбрать криптостойкий ключ
• Урок 3. Современные отечественные шифры. Что тaкое сеть Фейстеля, какими бывают отечественные блочные шифры, используемые в современных протоколах, — ГОСТ 28147—89, «Кузнечик»
• Урок 4. Современные зарубежные шифры. Что такое, как работают и в чем разница между 3DES, AES, Blowfish, IDEA, Threefish от Брюса Шнайдера
• Урок 5. Электронная подпись. Виды ЭП, как они работают и как их использовать
• Урок 6. Квантовая криптография. Что это такое, где используется и как помогает в распределении секретных ключей, генерации случайных чисел и электронной подписи