Сортировка методом пузырька в python
Содержание:
- Модификации[править]
- Использовать
- Метод пузырька
- Метод пузырьковой сортировки в Паскале
- Сортировка пузырьком
- Функция qsort из библиотеки stdlib[править]
- 2.4 Пирамидальная сортировка
- 2. Обзор алгоритмов сортировки
- Алгоритмы сортировки на собеседовании
- 1.2 Выбор программного обеспечения по реализации ИТ
- 2.1 Сортировка массива простыми включениями
- Заключение
Модификации[править]
Сортировка чет-нечетправить
Сортировка чет-нечет (англ. odd-even sort) — модификация пузырьковой сортировки, основанная на сравнении элементов стоящих на четных и нечетных позициях независимо друг от друга. Сложность — .
Псевдокод указан ниже:
function oddEvenSort(a):
for i = 0 to n - 1
if i mod 2 == 0
for j = 2 to n - 1 step 2
if a < a
swap(a, a)
else
for j = 1 to n - 1 step 2
if a < a
swap(a, a)
Преимущество этой сортировки — на нескольких процессорах она выполняется быстрее, так как четные и нечетные индексы сортируются параллельно.
Сортировка расческойправить
Сортировка расческой (англ. comb sort) — модификация пузырьковой сортировки, основанной на сравнении элементов на расстоянии. Сложность — , но стремится к . Является самой быстрой квадратичной сортировкой. Недостаток — она неустойчива. Псевдокод указан ниже:
function combSort(a): k = 1.3 jump = n bool swapped = true while jump > 1 and swapped if jump > 1 jump /= k swapped = false for i = 0 to size - jump - 1 if a < a swap(a, a) swapped = true
Пояснения: Изначально расстояние между сравниваемыми элементами равно , где — оптимальное число для этого алгоритма. Сортируем массив по этому расстоянию, потом уменьшаем его по этому же правилу. Когда расстояние между сравниваемыми элементами достигает единицы, массив досортировывается обычным пузырьком.
Сортировка перемешиваниемправить
Сортировка перемешиванием (англ. cocktail sort), также известная как Шейкерная сортировка — разновидность пузырьковой сортировки, сортирующая массив в двух направлениях на каждой итерации. В среднем, сортировка перемешиванием работает в два раза быстрее пузырька. Сложность — , но стремится она к , где — максимальное расстояние элемента в неотсортированном массиве от его позиции в отсортированном массиве. Псевдокод указан ниже:
function shakerSort(a):
begin = -1
end = n - 2
while swapped
swapped = false
begin++
for i = begin to end
if a > a
swap(a, a)
swapped = true
if !swapped
break
swapped = false
end--
for i = end downto begin
if a > a
swap(a, a)
swapped = true
Использовать
Пузырьковая сортировка — алгоритм сортировки, который непрерывно просматривает список, меняя местами элементы, пока они не появятся в правильном порядке. Список был построен в декартовой системе координат, где каждая точка ( x , y ) указывает, что значение y хранится в индексе x . Затем список будет отсортирован пузырьковой сортировкой по значению каждого пикселя
Обратите внимание, что сначала сортируется самый большой конец, а меньшим элементам требуется больше времени, чтобы переместиться в правильное положение.
Хотя пузырьковая сортировка является одним из самых простых алгоритмов сортировки для понимания и реализации, ее сложность O ( n 2 ) означает, что ее эффективность резко снижается в списках, состоящих из более чем небольшого числа элементов. Даже среди простых алгоритмов сортировки O ( n 2 ) такие алгоритмы, как сортировка вставкой , обычно значительно более эффективны.
Из-за своей простоты пузырьковая сортировка часто используется для знакомства с концепцией алгоритма или алгоритма сортировки для начинающих студентов- информатиков . Тем не менее, некоторые исследователи, такие как Оуэн Астрахан , пошли на многое, чтобы осудить пузырьковую сортировку и ее неизменную популярность в образовании по информатике, рекомендуя даже не преподавать ее.
Жаргон Файл , который лихо звонков bogosort «архетипический извращенно ужасный алгоритм», также вызывает пузырьковую сортировку «общий плохой алгоритм». Дональд Кнут в своей книге «Искусство компьютерного программирования» пришел к выводу, что «пузырьковой сортировке, похоже, нечего рекомендовать, кроме броского названия и того факта, что она приводит к некоторым интересным теоретическим проблемам», некоторые из которых он затем обсуждает.
Пузырьковая сортировка асимптотически эквивалентна по времени работы сортировке вставкой в худшем случае, но эти два алгоритма сильно различаются по количеству необходимых перестановок. Экспериментальные результаты, такие как результаты Astrachan, также показали, что сортировка вставкой работает значительно лучше даже в случайных списках. По этим причинам многие современные учебники алгоритмов избегают использования алгоритма пузырьковой сортировки в пользу сортировки вставкой.
Пузырьковая сортировка также плохо взаимодействует с современным оборудованием ЦП. Он производит как минимум вдвое больше записей, чем сортировка вставкой, вдвое больше промахов в кеш и асимптотически больше ошибочных прогнозов переходов . Эксперименты с сортировкой строк Astrachan в Java показывают, что пузырьковая сортировка примерно в пять раз быстрее сортировки вставкой и на 70% быстрее сортировки по выбору .
В компьютерной графике пузырьковая сортировка популярна благодаря своей способности обнаруживать очень маленькую ошибку (например, замену всего двух элементов) в почти отсортированных массивах и исправлять ее с линейной сложностью (2 n ). Например, он используется в алгоритме заполнения многоугольника, где ограничивающие линии сортируются по их координате x в определенной строке сканирования (линия, параллельная оси x ), а с увеличением y их порядок изменяется (два элемента меняются местами) только при пересечения двух линий. Пузырьковая сортировка — это стабильный алгоритм сортировки, как и сортировка вставкой.
Метод пузырька
Сортировка пузырьком в основном применяется в учебных проектах. В реальной практике её заменяют более эффективные алгоритмы, однако сортировка пузырьком лежит в основе некоторых из них.
В общем случае алгоритм сортировки пузырьком следующий:
- Сравнить текущий элемент со следующим.
- Если следующий элемент меньше/больше текущего, поменять их местами.
- Если массив отсортирован, закончить алгоритм, иначе перейти на шаг 1.
В алгоритме используется два цикла: основной и вложенный. В результате одного прохода вложенного цикла наибольший элемент помещается в конец массива, а наименьший смещается на одну позицию ближе к началу.
Внешний цикл в худшем случае совершает N (кол-во элементов) – 1 проходов, то есть внутренний цикл выполняется N-1 раз.
Таким образом, в каждом проходе совершается серия обменов элементов так, что наибольший элемент передвигается в конец массив перед элементом, который переместился туда в прошлой итерации. Процесс происходит до тех пор, пока массив не будет отсортирован.
Если рассмотреть реализацию алгоритма, то можно легко заметить, что время его работы (количество операций) значительно возрастает с увеличением количества элементов сортируемой последовательности.
Метод пузырьковой сортировки в Паскале
Замечание 1
Под сортировкой на языке Паскаль понимается упорядочение массива данных (как правило по возрастанию или по убыванию). Сортировка названа пузырьковой из-за аналогии с погруженными в воду вертикальным массивом. Массив — это вода, а его самые маленькие элементы являются пузырьками, которые стремятся всплыть вверх.
Алгоритм может быть представлен следующим образом:
-
Для выполнения процесса сортировки применяются два цикла, причём один цикл вложен в другой. Первый цикл применяется для формирования шагов, второй — под-шагов.
-
Основой алгоритма является сравнение двух элементов. К примеру, есть массив с десятью элементами. Элементы подлежат сравнению парами: 1 и 2, 2 и 3, 3 и 4 ,4 и 5 ,6 и 7 и так далее. Если при выполнении сравнения текущий элемент больше по величине чем следующий, то они меняются местами. К примеру, если первый элемент пять, а второй два, то они меняются местами.
-
Процесс сортировки пузырьковым методом подразделяется на шаги. Каждый шаг предполагает сравнение пары элементов. Итогом работы каждого шага является выстраивание самого большого элемента в конец массива. Таким образом после первого шага наибольший элемент массива окажется на последнем месте. При втором шаге действия выполняются по отношению ко всем элементам, исключая последний. Далее снова ищется наибольший элемент, и он перемещается опять в окончание массива, который в данный момент обрабатывается. И так процесс повторяется до полного окончания сортировки.
Приведём наглядный пример. Имеется массив, включающий в себя семь элементов: 2, 5, 11, 1, 7, 8, 3. Процесс сортировки изображён на рисунке 1.
 Рисунок 1. Процесс сортировки. Автор24 — интернет-биржа студенческих работ
Рисунок 1. Процесс сортировки. Автор24 — интернет-биржа студенческих работ
Далее сформируем собственно программу, реализующую данный алгоритм на языке Паскаль. Ниже приведён текст программы:
Замечание 2
Следует подчеркнуть, что элемент k нужен только для того, чтобы выполнить обмен местами двух элементов. Это объясняется тем, что Паскаль не имеет команды, которая смогла бы осуществить эту операцию. Это вынуждает формировать данную процедуру программным путём, вводя добавочный элемент для обмена.
Сортировка пузырьком
Идея алгоритма очень простая. Идём по массиву чисел и проверяем порядок (следующее число должно быть больше и равно предыдущему), как только наткнулись на нарушение порядка, тут же обмениваем местами элементы, доходим до конца массива, после чего начинаем сначала.
Отсортируем массив {1, 5, 2, 7, 6, 3}
Идём по массиву, проверяем первое число и второе, они идут в порядке возрастания. Далее идёт нарушение порядка, меняем местами эти элементы
Продолжаем идти по массиву, 7 больше 5, а вот 6 меньше, так что обмениваем из местами
3 нарушает порядок, меняем местами с 7
Возвращаемся к началу массива и проделываем то же самое
void bubbleSort(int *a, size_t size) {
size_t i, j;
int tmp;
for (i = 1; i < size; i++) {
for (j = 1; j < size; j++) {
if (a > a) {
tmp = a;
a = a;
a = tmp;
}
}
}
}
Этот алгоритм всегда будет делать (n-1)2 шагов, независимо от входных данных. Даже если массив отсортирован, всё равно он будет пройден (n-1)2 раз. Более того, будут в очередной раз проверены уже отсортированные данные.
Пусть нужно отсортировать массив 1, 2, 4, 3
После того, как были поменяны местами элемента a и a нет больше необходимости проходить этот участок массива
Примем это во внимание и переделаем алгоритм
void bubbleSort2(int *a, size_t size) {
size_t i, j;
int tmp;
for (i = 1; i < size; i++) {
for (j = i; j > 0; j--) {
if (a < a) {
tmp = a;
a = a;
a = tmp;
}
}
}
}
Ещё одна реализация
void bubbleSort2b(int *a, size_t size) {
size_t i, j;
int tmp;
for (i = 1; i < size; i++) {
for (j = 1; j <= size-i; j++) {
if (a < a) {
tmp = a;
a = a;
a = tmp;
}
}
}
}
В данном случае будет уже вполовину меньше шагов, но всё равно остаётся проблема сортировки уже отсортированного массива: нужно сделать так, чтобы отсортированный массив функция просматривала один раз. Для этого введём переменную-флаг: он будет опущен (flag = 0), если массив отсортирован. Как только мы наткнёмся на нарушение порядка, то флаг будет поднят (flag = 1) и мы начнём сортировать массив как обычно.
void bubbleSort3(int *a, size_t size) {
size_t i;
int tmp;
char flag;
do {
flag = 0;
for (i = 1; i < size; i++) {
if (a < a) {
tmp = a;
a = a;
a = tmp;
flag = 1;
}
}
} while (flag);
}
В этом случае сложность также порядка n2, но в случае отсортированного массива будет всего один проход.
Теперь усовершенствуем алгоритм. Напишем функцию общего вида, чтобы она сортировала массив типа void. Так как тип переменной не известен, то нужно будет дополнительно передавать размер одного элемента массива и функцию сравнения.
int intSort(const void *a, const void *b) {
return *((int*)a) > *((int*)b);
}
void bubbleSort3g(void *a, size_t item, size_t size, int (*cmp)(const void*, const void*)) {
size_t i;
void *tmp = NULL;
char flag;
tmp = malloc(item);
do {
flag = 0;
for (i = 1; i < size; i++) {
if (cmp(((char*)a + i*item), ((char*)a + (i-1)*item))) {
memcpy(tmp, ((char*)a + i*item), item);
memcpy(((char*)a + i*item), ((char*)a + (i-1)*item), item);
memcpy(((char*)a + (i-1)*item), tmp, item);
flag = 1;
}
}
} while (flag);
free(tmp);
}
Функция выглядит некрасиво – часто вычисляется адрес текущего и предыдущего элемента. Выделим отдельные переменные для этого.
void bubbleSort3gi(void *a, size_t item, size_t size, int (*cmp)(const void*, const void*)) {
size_t i;
void *tmp = NULL;
void *prev, *cur;
char flag;
tmp = malloc(item);
do {
flag = 0;
i = 1;
prev = (char*)a;
cur = (char*)prev + item;
while (i < size) {
if (cmp(cur, prev)) {
memcpy(tmp, prev, item);
memcpy(prev, cur, item);
memcpy(cur, tmp, item);
flag = 1;
}
i++;
prev = (char*)prev + item;
cur = (char*)cur + item;
}
} while (flag);
free(tmp);
}
Теперь с помощью этих функций можно сортировать массивы любого типа, например
void main() {
int a = {1, 0, 9, 8, 7, 6, 2, 3, 4, 5};
int i;
bubbleSort3gi(a, sizeof(int), 10, intSort);
for (i = 0; i < 10; i++) {
printf("%d ", a);
}
_getch();
}
Функция qsort из библиотеки stdlib[править]
Два оператора for, в которых происходит сортировка, можно заменить на одну строку:
Это функция, описанная в стандартной библиотеке ANSI C и объявлена в заголовочном файле stdlib.h.
Поэтому в начале программы нужно добавить
Функцией можно упорядочивать объекты любой природы. По сути, она предназначена упорядочивать множества блоков байтов равной длины.
Второй аргумент функции — это число таких блоков, третий аргумент — длина каждого блока.
Первый аргумент — это адрес, где находится начало первого блока (предполагается, что блоки в памяти расположены друг за другом подряд).
Четвёртый аргумент функции qsort — это имя функции, которая умеет сравнивать
два элемента массива. В нашем случае это
int cmp(const void *a, const void *b) {
return *(int*)a - *(int*)b;
}
В силу указанной универсальности функции сортировки, функция сравнения получает в качества аргумента адреса двух блоков, которые нужно сравнить и возвращает 1, 0 или -1:
- положительное значение, если a > b
- 0, если a == b
- отрицательное значение, если a < b
Поскольку у нас блоки байт — это целые числа (в 32-битной архитектуре это четырёхбайтовые блоки), то
необходимо привести данные указатели типа (const void*) к типу (int *) и осуществляется это с помощью дописывания
перед указателем выражения «(const int*)». Затем нужно получить значение переменной типа int, которая лежит по этому адресу.
Это делается с помощью дописывания спереди звездочки.
Таким образом, мы получили следующую программу
#include <stdio.h>
#include <stdlib.h>
#define N 1000
int cmp(const void *a, const void *b) {
return *(int*)a - *(int*)b;
}
int main() {
int n, i,j;
int aN];
scanf("%d", &n);
for(i = ; i < n; i++) { // ЧИТАЕМ ВХОД
scanf("%d", &ai]);
}
qsort(a, n, sizeof(int), cmp ); // СОРТИРУЕМ
for(i = ; i < n; i++) { // ВЫВОДИМ РЕЗУЛЬТАТ
printf("%d ", ai]);
}
return ;
}
2.4 Пирамидальная сортировка
Пирамида определяется как последовательность ключей
hl, hl+1,…, hr, такая, что hi <= h2i, hi <= h2i+1
для всякого i =l,…,r/2. Если двоичное дерево представлено в виде массива, как показано на рис.1, то, следовательно, деревья сортировки на рис.2 и 3 являются пирамидами, и, в частности, элемент h1 пирамиды является ее наименьшим элементом h1 = min (h1… hn).
Теперь предположим, что дана пирамида с элементами hl+1,…, hr для некоторых значений l и r и нужно добавить новый элемент x для того, чтобы сформировать расширенную пирамиду hl,…, hr. Возьмем, например, исходную пирамиду h1,…,h7, показанную на рис.2, и расширим эту пирамиду «влево», добавив элемент h1=44. Новый элемент x сначала помещается в вершину дерева, а затем «просеивается» по пути, на котором находятся меньшие по сравнению с ним элементы, которые одновременно поднимаются вверх; таким образом формируется новая пирамида. На рисунке 8 продемонстрирована пирамидальная сортировка.
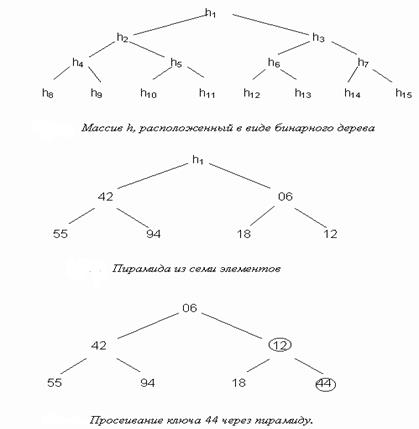
Рисунок 8. Процесс построения дерева
В данном примере значение 44 сначала меняется местами с 06, затем 12, и так формируется дерево. Далее процесс просеивания будем формулировать следующим образом: i, j — пара индексов, обозначающих элементы, которые нужно менять местами на каждом шаге просеивания.
Для восьми элементов из нашего примера минимальное и максимальное количества пересылок дают следующие исходные последовательности:
Мmin = 13 для последовательности
94, 67, 44, 55, 12, 42, 18, 6
Mmax=24 для последовательности
18, 42, 12, 44, 6, 55, 67, 94
Среднее число пересылок равно приблизительно nlog (n) /2 и отклонения от этого значения сравнительно малы.
2. Обзор алгоритмов сортировки
Сортировка — это процесс перестановки объектов данного множества в определённом порядке. Цель сортировки — облегчить последующий поиск элементов в отсортированном множестве. Поэтому элементы сортировки присутствуют во многих задачах прикладного программирования.
Рассмотрим алгоритмы сортировки «на месте», то есть те алгоритмы в которых не используется копирование массива.
Удобной мерой эффективности алгоритмов сортировки «на месте» является число необходимых сравнений в ходе сортировки и число необходимых пересылок элементов.
Эффективные алгоритмы сортировки требуют порядка
сравнений, где N — число элементов, а С — число необходимых сравнений.
Мы рассмотрим простые методы сортировки, которые требуют число сравнений порядка
Методы сортировки «на месте» можно разбить на три основных класса:
сортировка выбором
сортировка вставками
сортировка обменом
В сортировке выбором выбирается элемент с наибольшим значением ключа и меняется местами с последним. Затем то же самое повторяется для s-1 элемента. Найденный элемент с наибольшим значением ключа меняется
Рисунок 1. Сортировка простым выбором
В сортировке включениями элементы разделяются на уже упорядоченную и неупорядоченную последовательности. В начале упорядоченная часть содержит только один элемент. Очередной элемент из начала неупорядоченной части вставляется на подходящее место в упорядоченную часть. При этом упорядоченная часть удлиняется на один элемент, а неупорядоченная — укорачивается. Сортировка заканчивается при исчезновении неупорядоченной части (рисунок 2).
Рисунок 2. Сортировка простыми включениями
Основная характеристика сортировки обменом — перестановка местами двух соседних элементов, если они расположены не так, как требует отсортированный массив.
Рисунок 3. Сортировка простым обменом
В рассмотренной классификации существуют разные алгоритмы. Они отличаются сложностью, быстротой выполнения, последовательностью операций.
Например:
сортировка вставками;
пузырьковая сортировка;
корневая сортировка;
пирамидальная сортировка;
быстрая сортировка;
сортировка Шелла и др.
Рассмотрим подробнее основные типы и виды сортировок (сначала простые сортировки затем более сложные).
Сортировка массива простым выбором
Метод основан на следующем правиле:
Выбирается элемент с наибольшим значением ключа
Он меняется местами с последним элементом arr . Затем эти операции повторяются с оставшимися первыми s-1 элементами, затем — с s-2 первыми элементами и т.д. до тех пор, пока не останется только первый элемент — наименьший. Пример сортировки методом простого выбора показан на рисунке 4:
Рисунок 4. Сортировка массива простым выбором
Эффективность сортировки простым выбором. Число сравнений ключей не зависит от начального порядка ключей. Операция сравнения выполняется в теле цикла с управляющей переменной k
и средним числом повторений size/2. Этот цикл, в свою очередь, находится в теле цикла с управляющей переменной L
и числом повторений size −1. Таким образом, число сравнений
С= (size −1) * size −1/2
Число пересылок, напротив, зависит от начального порядка ключей. Если принять, что операция сравнения в теле цикла по k
дает результат «истина» в половине случаев, то среднее число пересылок в этом цикле равно size/4. Цикл по L
, как указывалось выше, выполняется size −1 раз и в теле цикла выполняется три пересылки и цикл по k
. С учетом этого число пересылок:
М= (3+ size/4) * (size −1)
Получаем, что при сортировке простым выбором и число сравнений, и число пересылок пропорционально .
Алгоритмы сортировки на собеседовании
Алгоритмов сортировки достаточно много, и вряд ли можно встретить программиста, который может по памяти написать реализацию хотя бы половины из них.
На самом деле, программисты просто гуглят необходимую реализацию. Конечно, они имеют представление о принципах их работы, потому что в своё время рассмотрели несколько алгоритмов, как, например, сортировка пузырьком.
Кроме того, в Python и других языках программирования существуют встроенные функции, которые производят сортировку быстро и эффективно.
На собеседованиях спрашивают про алгоритмы сортировки, но это не значит, что от будущего работника требуют написать их реализацию или придумать свой. Работодатель требует от специалиста следующее:
- Уметь классифицировать алгоритмы сортировки.
- Знать преимущества и недостатки популярных алгоритмов, чтобы понимать, когда каждый из них лучше использовать.
- Понимать, что такое сложность алгоритма и как с её помощью определять, подходит ли он для решения данной задачи.
1.2 Выбор программного обеспечения по реализации ИТ
При написании программ для реализации сортировок массивов был использован язык программирования С++. Это один из широко используемых языков программирования, который можно использовать для написания программ, работающих в операционной среде Windows. Среда Borland C++ Builder 6- это сложный механизм, обеспечивающий высокоэффективную работу программиста
Интегрированная среда разработки C++ Builder представляет собой многооконную систему. Вид интегрированной среды разработки (интерфейс) может различаться в зависимости от настроек. Кроме стандартных окон, на экране могут присутствовать и другие окна, отображаемые при вызове соответствующих средств, например, Image Editor (Редактор изображений). Окна C++ Builder (но не главное) можно перемещать, убирать с экрана, а также изменять их размеры.
Несмотря на наличие многих окон, C++ Builder является одно-документной средой, т.е. позволяет одновременно работать только с одним приложением (проектом приложения). Название проекта приложения выводится в строке заголовка главного окна в верхней части экрана.
Если свернуть главное окно, то происходит минимизация всего интерфейса C++ Builder и, соответственно, всех открытых окон. При закрытии главного окна работа с C++ Builder прекращается.
Borland C++ Builder 6, вобрав в себя всё самое лучшее от предыдущих версий, предоставляет ряд новых возможностей. Так, например, стал более удобным и современным интерфейс среды программирования, создаваемые C++ Builder программы учитывают архитектуру современных процессоров, существенно расширены возможности отладчика.
Borland C++ Builder 6 может работать в среде операционных систем от Windows 95 до Windows XP. Особенных требований к компьютеру система не предъявляет, за исключением того, что процессор должен быть типа Pentium, оперативной памяти — не менее 32 Мбайт и достаточное количество свободной дисковой памяти.
2.1 Сортировка массива простыми включениями
Метод простых вставок предполагает разделение всего массива элементов на упорядоченную часть, которая вначале содержит лишь один элемент, и неупорядоченную. Очередной элемент из неупорядоченной части вставляется в определенное место упорядоченной части, проходя сравнение с ее элементами. При поиске подходящего места удобно чередовать сравнения и пересылки, т.е. как бы «просеивать» выбранный элемент, сравнивая его с очередным элементом a и либо вставляя, либо пересылая a направо и продвигаясь налево. Заметим, что «просеивание» может закончиться при двух различных условиях: найден элемент a с ключом меньшим, чем ключ x или достигнут левый конец готовой последовательности.
При этом упорядоченная часть удлиняется на один элемент. Сортировка заканчивается при окончании неупорядоченной части.
При данной сортировке общее число сравнений приблизительно равно
,
При этом требуется количество проходов по данным P
 |
Рисунок 5. Пример сортировки массива простыми включениями
Число Ci сравнений ключей при i-м просеивании составляет самое большее i-1, самое меньшее 1 и, если предположить, что все перестановки n ключей равновероятны, в среднем равно i/2. Число Мi пересылок (присваиваний) равно Ci+2 (учитывая барьер). Поэтому общее число сравнений и пересылок есть
Cmin = n-1 Mmin = 2 (n-1)
Cср. = (n2+n-2) /4 Mср. = (n2+9n-10) /4
Cmax = ( (n2+n) — 1) /2 Mmax = (n2+3n-4) /2.
Алгоритм сортировки простыми включениями можно легко улучшить, пользуясь тем, что готовая последовательность a ,…, a , в которую нужно включить новый элемент, уже упорядочена. Поэтому место включения можно найти значительно быстрее, применив бинарный поиск, который исследует средний элемент готовой последовательности и продолжает деление пополам, пока не будет найдено место включения.
Заключение
Метод пузырька гораздо менее эффективен других алгоритмов, однако он имеет простую и понятную реализацию, поэтому часто используется в учебных целях. Кроме того, пузырьковая сортировка может использоваться для работы с небольшими массивами данных.
На самом деле, вместо самостоятельного написания алгоритмов сортировки программисты на Python используют стандартные функции и методы языка, такие как и . Эти функции отлажены и работают быстро и эффективно.
Знания особенностей алгоритмов сортировки, их сложности и принципов реализации в общем виде пригодятся каждому программисту, желающему пройти собеседование и стать Python-разработчиком.