Round (transact-sql)round (transact-sql)

Встроенные функции

Для операции округления в Python есть встроенные функции – и

round

– округляет число (number) до ndigits знаков после запятой. Это стандартная функция, которая для выполнения не требует подключения модуля math.

По умолчанию операция проводится до нуля знаков – до ближайшего целого числа. Например:

Чтобы получить целый показатель, результат преобразовывают в .

Синтаксически функция вызывается двумя способами.

1. – это округление числа до целого, которое расположено ближе всего. Если дробная часть равна 0,5, то округляют до ближайшего четного значения.
2. – данные округляют до знаков после точки. Если округление проходит до сотых, то равен «2», если до тысячных – «3» и т.д.

int

– встроенная функция, не требующая подключения дополнительных модулей. Её функция – преобразование действительных значений к целому путем округления в сторону нуля. Например

Для положительных чисел функция аналогична функции , а для отрицательных – аналогично . Например:

Чтобы число по int преобразовать по математическим правилам, нужно выполнить следующие действия.

1. Если число положительное, добавить к нему 0,5.
2. Если число отрицательное, добавить -0,5.

Синтаксически преобразование оформляется так:

5 Интересный факт о strictfp

В Java есть специальное ключевое слово (strict floating point), которого нет в других языках программирования. И знаете, зачем оно нужно? Оно ухудшает точность работы с вещественными числами. История его появления примерно такова:

Создатели Java:

Мы очень хотим, чтобы Java была суперпопулярна, и программы на Java выполнялись на как можно большем количестве устройств. Поэтому мы прописали в спецификацию Java-машины, что на всех типах устройств все программы должны выполняться одинаково!

Создатели процессора Intel:

Ребята, мы улучшили наши процессоры? и теперь все вещественные числа внутри процессора будет представлены не 8-ю, а 10-ю байтами. Больше байт — больше знаковых цифр. А это значит что? Правильно: теперь ваши научные вычисления будут еще более точными!

Ученые и все, кто занимается сверхточными расчетами:

Круто! Молодцы. Отличная новость.

Создатели Java:

Не-не-не, ребята. Мы же сказали: все Java-программы должны выполняться одинаково на всех устройствах. Принудительно выключаем возможность использования 10 байтовых вещественных чисел внутри процессоров Intel.

Вот теперь все опять отлично! Не благодарите.

Ученые и все, кто занимается сверхточными расчетами:

Да вы там совсем охренели? А ну быстро вернули все как было!

Создатели Java:

Ребята, это для вашей же пользы! Только представьте: все Java-программы выполняются одинаково на всех устройствах. Ну круто же!

Ученые и все, кто занимается сверхточными расчетами:

Нет. Совсем не круто. Быстро вернули все обратно! Или мы вашу Java вам знаете куда засунем?

Создатели Java:

Гм. Что же вы сразу не сказали. Конечно, вернем.

Вернули возможность пользоваться всеми фичами крутых процессоров.

Кстати. Мы так же специально добавили в язык слово : если его написать перед именем функции, вся работа с вещественными числами внутри этой функции будет одинаково плохой на всех устройствах!

Округление в большую сторону при условии в Excel

Пример 2. Балл за предмет в учебном заведении рассчитывается как среднее арифметическое баллов за 7 контрольных работ. При этом в пользу ученика округление в большую сторону выполняется в том случае, если дробная часть полученного числа >= 0,8. Определить оценку для ученика (используется 10-бальная шкала оценки знаний).

Исходные данные:

Формула для расчета:

То есть, если дробная часть числа, которое является средним арифметическим значением баллов за 7 контрольных, меньше, чем 0,8, итоговый балл будет рассчитан как ближайшее меньшее целое среднего балла, иначе – как ближайшее большее (в пользу ученика).

Результат вычислений:

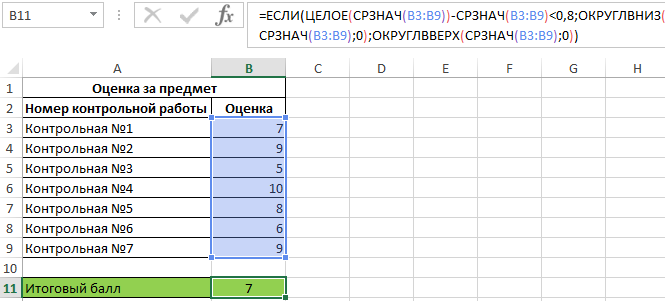
Ученик не получил «прибавку» к оценке, поскольку средний балл за контрольные составил 7,71 (0,71<0,8).

Округление при работе с числами ограниченной точности

Реальные физические величины всегда измеряются с некоторой конечной точностью, которая зависит от приборов и методов измерения и оценивается максимальным относительным или абсолютным отклонением неизвестного истинного значения от измеренного, что в десятичном представлении значения соответствует либо определённому числу значащих цифр, либо определённой позиции в записи числа, все цифры после (правее) которой являются незначащими (лежат в пределах погрешности измерения). Сами измеренные параметры записываются с таким числом знаков, чтобы все цифры были надёжными, возможно, последняя — сомнительной. Погрешность при математических операциях с числами ограниченной точности сохраняется и изменяется по известным математическим законам, поэтому когда в дальнейших вычислениях возникают промежуточные значения и результаты с больши́м числом цифр, из этих цифр только часть являются значимыми. Остальные цифры, присутствуя в значениях, фактически не отражают никакой физической реальности и лишь отнимают время на вычисления. Вследствие этого промежуточные значения и результаты при вычислениях с ограниченной точностью округляют до того количества знаков, которое отражает реальную точность полученных значений. На практике обычно рекомендуется при длинных «цепочных» ручных вычислениях сохранять в промежуточных значениях на одну цифру больше. При использовании компьютера промежуточные округления в научно-технических приложениях чаще всего теряют смысл, и округляется только результат.

Так, например, если задана сила 5815 гс с точностью до грамма силы и длина плеча 1,40 м с точностью до сантиметра, то момент силы в кгс по формуле M=(mg)⋅h{\displaystyle M=(mg)\cdot h}, в случае формального расчёта со всеми знаками, окажется равным: 5,815 кгс • 1,4 м = 8,141 кгс•м. Однако если учесть погрешность измерения, то мы получим, что предельная относительная погрешность первого значения составляет 1/5815 ≈ 1,7•10−4, второго — 1/140 ≈ 7,1•10−3, относительная погрешность результата по правилу погрешности операции умножения (при умножении приближённых величин относительные погрешности складываются) составит 7,3•10−3, что соответствует максимальной абсолютной погрешности результата ±0,059 кгс•м! То есть в реальности, с учётом погрешности, результат может составлять от 8,082 до 8,200 кгс•м, таким образом, в рассчитанном значении 8,141 кгс•м полностью надёжной является только первая цифра, даже вторая — уже сомнительна! Корректным будет округление результата вычислений до первой сомнительной цифры, то есть до десятых: 8,1 кгс•м, или, при необходимости более точного указания рамок погрешности, представить его в виде, округлённом до одного-двух знаков после запятой с указанием погрешности: 8,14 ± 0,06 кгс•м.

Округление рассчитанного значения погрешности

Обычно в окончательном значении рассчитанной погрешности оставляют только первые одну-две значащие цифры. По одному из применяемых правил, если значение погрешности начинается с цифр 1 или 2(по другому правилу — 1, 2 или 3), то в нём сохраняют две значащих цифры, в остальных случаях — одну, например: 0,13; 0,26; 0,3; 0,8. То есть каждая декада возможных значений округляемой погрешности разделена на две части. Недостаток этого правила состоит в том, что относительная погрешность округления изменяется значительным скачком при переходе от числа 0,29 к числу 0,3. Для устранения этого предлагается каждую декаду возможных значений погрешности делить на три части с менее резким изменением шага округления. Тогда ряд разрешённых к употреблению округлённых значений погрешности получает вид:

• 0,10; 0,12; 0,14; 0,16; 0,18;
• 0,20; 0,25; 0,30; 0,35; 0,40; 0,45;
• 0,5; 0,6; 0,7; 0,8; 0,9; 1,0.

Однако при использовании такого правила последние цифры самого результата, оставляемые после округления, также должны соответствовать приведённому ряду.

Пересчёт значений физических величин

Пересчёт значения физической величины из одной системы единиц в другую должен производиться с сохранением точности исходного значения. Для этого исходное значение в одних единицах следует умножить (разделить) на переводной коэффициент, часто содержащий большое количество значащих цифр, и округлить полученный результат до количества значащих цифр, обеспечивающего точность исходного значения. Например, при пересчёте значения силы 96,3 тс в значение, выраженное в килоньютонах (кН), следует умножить исходное значение на переводной коэффициент 9,80665 (1 тс = 9,80665 кН). В результате получается значение 944,380395 кН, которое необходимо округлить до трёх значащих цифр. Вместо 96,3 тс получаем 944 кН.

ПримерыExamples

A.A. Использование функции ROUND и приближенийUsing ROUND and estimates

Следующий пример показывает два выражения, которые демонстрируют, используя , что последний знак всегда является приближением.The following example shows two expressions that demonstrate by using the last digit is always an estimate.

Результирующий набор:Here is the result set.

В следующем примере показаны округление и аппроксимация.The following example shows rounding and approximations.

Результирующий набор:Here is the result set.

В.C. Использование функции ROUND для усеченияUsing ROUND to truncate

В следующем примере используются две инструкции для демонстрации различия между округлением и усечением.The following example uses two statements to demonstrate the difference between rounding and truncation. Первая инструкция округляет результат.The first statement rounds the result. Вторая инструкция усекает результат.The second statement truncates the result.

Результирующий набор:Here is the result set.

Приближённые значения

Приближённые (или приблизительные) значения применяются тогда, когда точное значение чего-то найти невозможно, или же не важно чтобы это значение было точным для исследуемого предмета. Например, на словах можно сказать, что в городе проживает полмиллиона человек, но это высказывание не будет истинным, поскольку количество человек в городе меняется — люди приезжают и уезжают, рождаются и умирают

Поэтому правильнее будет сказать, что в городе проживает приблизительно полмиллиона человек

Например, на словах можно сказать, что в городе проживает полмиллиона человек, но это высказывание не будет истинным, поскольку количество человек в городе меняется — люди приезжают и уезжают, рождаются и умирают. Поэтому правильнее будет сказать, что в городе проживает приблизительно полмиллиона человек.

Ещё пример. В девять утра начинаются занятия. Мы вышли из дома в 8:30. Через некоторое время по дороге мы встретили своего товарища, который спросил у нас сколько сейчас времени. Когда мы выходили из дома было 8:30, на дорогу мы потратили какое-то неизвестное время. Мы не знаем сколько сейчас времени, поэтому отвечаем товарищу: «сейчас приблизительно около девяти часов».

В математике приближенные значения указываются с помощью специального знака. Выглядит он следующим образом:

Читается как «приближённо (приблизительно) равно».

Чтобы указать приближённое (приблизительное) значение, прибегают к такому действию как округление чисел.

Эмпирические правила арифметики с округлениями

В тех случаях, когда нет необходимости в точном учёте вычислительных погрешностей, а требуется лишь приблизительно оценить количество точных цифр в результате расчёта по формуле, можно пользоваться набором простых правил округлённых вычислений:

Все исходные значения округляются до реальной точности измерений и записываются с соответствующим числом значащих цифр, так, чтобы в десятичной записи все цифры были надёжными (допускается, чтобы последняя цифра была сомнительной). При необходимости значения записываются со значащими правыми нулями, чтобы в записи указывалось реальное число надёжных знаков (например, если длина в 1 м реально измерена с точностью до сантиметров, записывается «1,00 м», чтобы было видно, что в записи надёжны два знака после запятой), или точность явно указывается (например, 2500±5 м — здесь надёжными являются только десятки, до них и следует округлять).
Промежуточные значения округляются с одной «запасной» цифрой.
При сложении и вычитании результат округляется до последнего десятичного знака наименее точного из параметров (например, при вычислении значения 1,00 м + 1,5 м + 0,075 м результат округляется до десятых метра, то есть до 2,6 м). При этом рекомендуется выполнять вычисления в таком порядке, чтобы избегать вычитания близких по величине чисел и производить действия над числами по возможности в порядке возрастания их модулей.
При умножении и делении результат округляется до наименьшего числа значащих цифр, которое имеют множители или делимое и делитель

Например, если тело при равномерном движении прошло дистанцию 2,5 × 103 метров за 635 секунд, то при вычислении скорости результат должен быть округлён до 3,9 м/с, поскольку одно из чисел (расстояние) известно лишь с точностью до двух значащих цифр.

Важное замечание: если один операндов при умножении или делитель при делении является по смыслу целым числом (то есть не результатом измерений непрерывной физической величины с точностью до целых единиц, а, например, количеством или просто целой константой), то количество значащих цифр в нём на точность результата операции не влияет, и оставляемое число цифр определяется только вторым операндом. Например, кинетическая энергия тела массой 0,325 кг, движущегося со скоростью 5,2 м/с, равна Ek=mv22=0.325⋅5.222=4.394≈4.4{\displaystyle E_{k}={\tfrac {mv^{2}}{2}}={\tfrac {0.325\cdot 5.2^{2}}{2}}=4.394\approx 4.4} Дж — округляется до двух знаков (по количеству значащих цифр в значении скорости), а не до одного (делитель 2 в формуле), так как значение 2 по смыслу — целая константа формулы, она является абсолютно точной и не влияет на точность вычислений (формально такой операнд можно считать «измеренным с бесконечным числом значащих цифр»).

При вычислении значения функции f(x){\displaystyle f\left(x\right)} требуется оценить значение модуля производной этой функции в окрестности точки вычисления

Если |f′(x)|⩽1{\displaystyle \left|f’\left(x\right)\right|\leqslant 1}, то результат функции точен до того же десятичного разряда, что и аргумент. В противном случае результат содержит меньше точных десятичных разрядов на величину log10⁡(|f′(x)|){\displaystyle \log _{10}\left(\left|f’\left(x\right)\right|\right)}, округлённую до целого в большую сторону.

Несмотря на нестрогость, приведённые правила достаточно хорошо работают на практике, в частности, из-за достаточно высокой вероятности взаимопогашения ошибок, которая при точном учёте погрешностей обычно не учитывается.

Обозначения

Операция округления числа x к большему (вверх) обозначается следующим образом: ⌈x⌉{\displaystyle \lceil x\rceil }. Аналогично, округление к меньшему (вниз) обозначается ⌊x⌋{\displaystyle \lfloor x\rfloor }. Эти символы (а также английские названия для этих операций — соответственно, ceiling и floor, досл. «потолок» и «пол») были введеныК. Айверсоном в его работе A Programming Language, описавшей систему математических обозначений, позже развившуюся в язык программирования APL. Айверсоновские обозначения операций округления были популяризированы Д. Кнутом в его книге «Искусство программирования».

По аналогии, округление к ближайшему целому часто обозначают как x{\displaystyle \left}. В некоторых прежних и современных (вплоть до конца XX века) работах так обозначалось округление к меньшему; такое использование этого обозначения восходит ещё к работе Гаусса 1808 года (третье его доказательство квадратичного закона взаимности). Кроме того, это же обозначение используется (с другим значением) в нотации Айверсона.

В стандарте Юникод зафиксированы следующие символы:

Названиев Юникоде	Код в Юникоде	Вид	Мнемоникав HTML 4	Примечания
16-ричный	десятичный
LEFT CEILING (тж. APL upstile)	2308	8968	⌈	⌈	не путать с: U+2E22 ⸢ — Top left half bracket U+300C 「 — Left corner bracket
RIGHT CEILING	2309	8969	⌉	⌉	не путать с: U+20E7 ◌⃧ — Combining annuity symbol U+2E23 ⸣ — Top right half bracket
LEFT FLOOR (тж. APL downstile)	230A	8970	⌊	⌊	не путать с:
RIGHT FLOOR	230B	8971	⌋	⌋	не путать с: U+2E25 ⸥ — Bottom right half bracket U+300D 」 — Right corner bracket

Округление в меньшую сторону при условии в Excel

Пример 4. Клиент взял кредит в МФО на сумму 10000 рулей и спустя 30 дней обязуется вернуть 16000 рублей. В результате пересмотрение договора, клиенту удалось добиться снижения суммы к возврату до 15000 рублей. Определить, как изменилась годовая процентная ставка (округленное значение разницы между прежней и новой ставкой до числа, кратного 10%).

Исходные данные:

Для расчета начальной ставки используем формулу:

Описание аргументов:

• B4 – число периодов;
• 0 – выплата за период (0, поскольку выплата только одна);
• B2 – тело кредита;
• B3 – сумма к возврату;
• 0 – оплата по окончанию периода;
• 0,01 – предположение (любое число из интервала от 0 до 1);
• 365/30 – выражение для пересчета годовой процентной ставки.

Полученный результат:

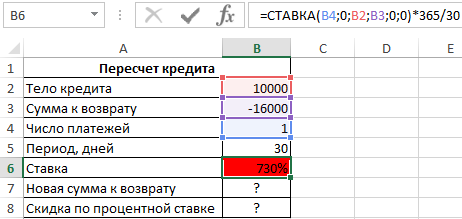
Для определения скидки используем формулу:

Описание аргументов:

• СТАВКА(B4;0;B2;B7;0;0,01)*365/30-B6 – округляемое значение (разница ставок);
• 10% — число, которому является кратным полученный результат.

Округление выполняется в сторону, большую по модулю, в результате имеем:

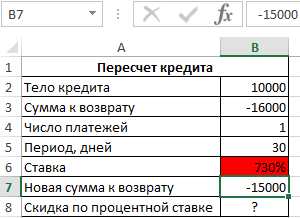
Полученное значение отличается от действительного на 8% (122% без округления), поэтому целесообразно явно указать аргумент :

В результате получим:

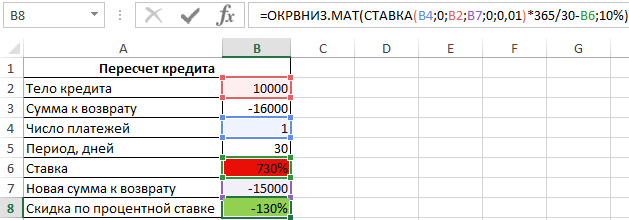
Аналогичный результат можно получить при использовании функции ОКРВВЕРХ.МАТ без явного указания аргумента :

Результат расчетов:

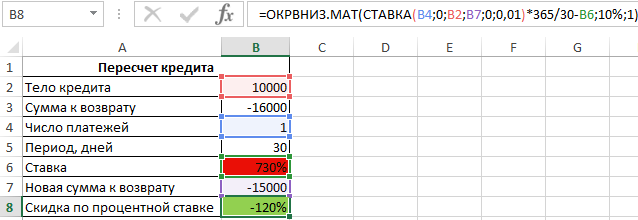
Примечание: следует помнить, что функции ОКРВВЕРХ.МАТ и ОКРВНИЗ.МАТ являются чувствительными к значениям, принимаемым вторым и третьим аргументами при округлении отрицательных чисел. Некоторые сочетания значений и приводят к различным результатам округления.

toString(base)

Метод возвращает строковое представление числа в системе счисления .

Например:

может варьироваться от до (по умолчанию ).

Часто используемые:

• base=16 — для шестнадцатеричного представления цвета, кодировки символов и т.д., цифры могут быть или .

• base=2 — обычно используется для отладки побитовых операций, цифры или .

• base=36 — максимальное основание, цифры могут быть или . То есть, используется весь латинский алфавит для представления числа. Забавно, но можно использовать -разрядную систему счисления для получения короткого представления большого числового идентификатора. К примеру, для создания короткой ссылки. Для этого просто преобразуем его в -разрядную систему счисления:

Две точки для вызова метода

Внимание! Две точки в это не опечатка. Если нам надо вызвать метод непосредственно на числе, как в примере выше, то нам надо поставить две точки после числа

Если мы поставим одну точку: , тогда это будет ошибкой, поскольку синтаксис JavaScript предполагает, что после первой точки начинается десятичная часть. А если поставить две точки, то JavaScript понимает, что десятичная часть отсутствует, и начинается метод.

Также можно записать как .

ПримерыExamples

A.A. Использование функции ROUND и приближенийUsing ROUND and estimates

Следующий пример показывает два выражения, которые демонстрируют, используя , что последний знак всегда является приближением.The following example shows two expressions that demonstrate by using the last digit is always an estimate.

Результирующий набор:Here is the result set.

В следующем примере показаны округление и аппроксимация.The following example shows rounding and approximations.

Результирующий набор:Here is the result set.

В.C. Использование функции ROUND для усеченияUsing ROUND to truncate

В следующем примере используются две инструкции для демонстрации различия между округлением и усечением.The following example uses two statements to demonstrate the difference between rounding and truncation. Первая инструкция округляет результат.The first statement rounds the result. Вторая инструкция усекает результат.The second statement truncates the result.

Результирующий набор:Here is the result set.

parseInt и parseFloat

Для явного преобразования к числу можно использовать или . Если строка не является в точности числом, то результат будет :

Единственное исключение — это пробелы в начале строки и в конце, они игнорируются.

В реальной жизни мы часто сталкиваемся со значениями у которых есть единица измерения, например или в CSS. Также во множестве стран символ валюты записывается после номинала . Так как нам получить числовое значение из таких строк?

Для этого есть и .

Они «читают» число из строки. Если в процессе чтения возникает ошибка, они возвращают полученное до ошибки число. Функция возвращает целое число, а возвращает число с плавающей точкой:

Функции вернут , если не смогли прочитать ни одну цифру:

Второй аргумент

Функция имеет необязательный второй параметр. Он определяет систему счисления, таким образом может также читать строки с шестнадцатеричными числами, двоичными числами и т.д.:

Примечания

1. ↑
2. Кнут Д. Э. Искусство программирования. Том 1. Основные алгоритмы = The Art of Computer Programming. Volume 1. Fundamental Algorithms / под ред. С. Г. Тригуб (гл. 1), Ю. Г. Гордиенко (гл. 2) и И. В. Красикова (разд. 2.5 и 2.6). — 3. — Москва: Вильямс, 2002. — Т. 1. — 720 с. — ISBN 5-8459-0080-8.
3. A’HEARN, B., J. BATEN AND D. CRAYEN (2009). “Quantifying Quantitative Literacy: Age Heaping and the History of Human Capital”, Journal of Economic History 69,783-808.
4. В. М. Заварыкин, В. Г. Житомирский, М. П. Лапчик. Техника вычислений и алгоритмизация: Вводный курс: Учебное пособие для студентов педагогических институтов по физико-математическим специальностям. — М: Просвещение, 1987. 160 с.: ил.
5. цит. по В. Гильде, З. Альтрихтер. «С микрокалькулятором в руках». Издание второе. Перевод с немецкого Ю. А. Данилова. М:Мир, 1987, стр. 64.

Различие округления в Python 2 и Python 3

В Python 2 и Python 3 реализованы разные принципы округления.

В Python 2 используется арифметическое округление. В нем наблюдается большое количество погрешностей, что приводит к неточностям в процессе вычислений.

Во втором Python есть только 4 цифры, которые ведут к преобразованию к меньшему значению – 1, 2, 3 и 4. Также 5 цифр, которые приводят к большему значению – 5, 6, 7, 8, 9. Такое неравное распределение ведет к тому, что погрешность постоянно нарастает.

Python 2 по правилам арифметического округления преобразует число 5,685 в 5,68 до второго знака. Такая погрешность связана с тем, что десятичные цифры float в двоичном коде невозможно корректно представить.

В Python 3 используются принципы банковского округления. Это означает, что преобразование производится к ближайшему четному. В таком случае также не удается полностью избежать возникающих ошибок, но программисты добиваются точности в подсчетах.

2,5 по правилам банковского преобразования будет равно 2, а 3,5 = 4 (значения возводятся к близкому четному). Минимизировать погрешности можно благодаря практически равной вероятности, что перед пятеркой будет четное или нечетное число.

Округление чисел

Для нахождения приближенного значения применяется такое действие как округление чисел.

Слово «округление» говорит само за себя. Округлить число значит сделать его круглым. Круглым называется число, которое оканчивается нулём. Например, следующие числа являются круглыми:

10, 20, 30, 100, 300, 700, 1000

Любое число можно сделать круглым. Процедуру, при которой число делают круглым, называют округлением числá.

Мы уже занимались «округлением» чисел, когда делили большие числа. Напомним, что для этого мы оставляли без изменения цифру, образующую старший разряд, а остальные цифры заменяли нулями. Но это были лишь наброски, которые мы делали для облегчения деления. Своего рода лайфхак. По факту, это даже не являлось округлением чисел. Именно поэтому в начале данного абзаца мы взяли слово округление в кавычки.

На самом деле, суть округления заключается в том, чтобы найти ближайшее значение от исходного. При этом, число может быть округлено до определённого разряда — до разряда десятков, разряда сотен, разряда тысяч.

Рассмотрим простой пример на округление. Дано число 17. Требуется округлить его до разряда десятков.

Не забегая вперёд попробуем понять, что означает «округлить до разряда десятков». Когда говорят округлить число 17, то надо понимать, что от нас требуют найти ближайшее круглое число от числá 17. Причём в ходе этого поиска возможно изменения коснутся и той цифры, которая располагается в разряде десятков числá 17 (т.е цифры 1).

Предстáвим числа от 10 до 20 с помощью следующего рисунка:

На рисунке видно, что для числá 17 ближайшее круглое число это число 20. Значит ответ к задаче таким и будет: «17 приближённо равно 20″

17 ≈ 20

Мы нашли приближённое значение для 17, то есть округлили его до разряда десятков. Видно, что после округления в разряде десятков появилась новая цифра 2.

Попробуем найти приближённое число для числа 12. Для этого снова предстáвим числа от 10 до 20 с помощью рисунка:

На рисунке видно, что ближайшее круглое число для 12 это число 10. Значит ответ к задаче таким и будет: 12 приближённо равно 10

12 ≈ 10

Мы нашли приближённое значение для 12, то есть округлили его до разряда десятков. В этот раз цифра 1, которая стояла в разряде десятков в числе 12, не пострадала от округления. Почему так получилось мы расскажем позже.

Попробуем найти ближайшее число для числá 15. Снова предстáвим числа от 10 до 20 с помощью рисунка:

На рисунке видно, что число 15 одинаково удалено от круглых чисел 10 и 20. Возникает вопрос: которое из этих круглых чисел будет приближённым значением для числа 15? Для таких случаев условились принимать бóльшее число за приближённое. 20 больше чем 10, поэтому приближённое значение для 15 будет число 20

15 ≈ 20

Округлять можно и большие числа. Естественно, для них делать рисунки и изображать числа не представляется возможным. Для них существует свой способ. Например, округлим число 1456 до разряда десятков.

Итак, мы должны округлить 1456 до разряда десятков. Разряд десятков начинается на пятёрке:

Теперь о существовании первых цифр 1 и 4 временно забываем. Остается число 56

Теперь смотрим, какое круглое число находится ближе к числу 56. Очевидно, что ближайшее круглое число для 56 это число 60. Значит заменяем число 56 на число 60

Значит при округлении числа 1456 до разряда десятков полýчим 1460

1456 ≈ 1460

Видно, что после округления числа 1456 до разряда десятков, изменения коснулись и самогó разряда десятков. В новом полученном числе в разряде десятков теперь располагается цифра 6, а не 5.

Округлять числа можно не только до разряда десятков. Округлять число можно до разряда сотен, тысяч, десятков тысяч и так далее.

После того, как станóвится ясно, что округление это ни что иное как поиск ближáйшего числá, можно применять готовые правила, которые значительно облегчают округление чисел.

Округлить до 1000 руб.

Функция Round() в Excel принимает отрицательные числа в качестве количества мест от запятой, напр. Round(123456, -3) округляет до 1000. К сожалению, аксессовская функция этого не поддерживает.

Чтобы округлить до ближайших 1000 руб., разделите на 1000, округлите, и умножьте на 1000. Пример:    1000 * Round( / 1000, 0)

Чтобы округлить до 1000 руб. вниз, разделите на 1000, получите целое число и умножьте на 1000. Пример:    1000 * Int( / 1000)

Чтобы округлить до верхней 1000 руб., разделите на 1000 и умножьте на -1 перед получением целой величины. Пример:    -1000 * Int( / -1000)

Чтобы округлить в сторону нуля, используйте Fix() вместо Int().

Альтернативно, пользовательская функция Кена Гетца ведет себя в точности как упомнутая экселевская функция.

Комментарии

Поведение этого метода соответствует стандарту IEEE 754, разделу 4.The behavior of this method follows IEEE Standard 754, section 4. Этот тип округления иногда называют округлением в сторону отрицательной бесконечности.This kind of rounding is sometimes called rounding toward negative infinity.

Floor(Double)

Возвращает наибольшее целое число, которое меньше или равно заданному числу с плавающей запятой двойной точности.Returns the largest integral value less than or equal to the specified double-precision floating-point number.

d

Double

Число двойной точности с плавающей запятой.A double-precision floating-point number.

Возвращаемое значение

Double

Наибольшее целое число, которое меньше или равно .The largest integral value less than or equal to . Если значение параметра равно NaN, NegativeInfinity или PositiveInfinity, возвращается это значение.If is equal to NaN, NegativeInfinity, or PositiveInfinity, that value is returned.

Примеры

В следующем примере показан метод и его отличие от метода.The following example illustrates the method and contrasts it with the method.

Комментарии

Поведение этого метода соответствует стандарту IEEE 754, разделу 4.The behavior of this method follows IEEE Standard 754, section 4. Этот тип округления иногда называют округлением в сторону отрицательной бесконечности.This kind of rounding is sometimes called rounding toward negative infinity. Иными словами, если является положительным, любой дробный компонент усекается.In other words, if is positive, any fractional component is truncated. Если имеет отрицательное значение, присутствие любого компонента дробной части приводит к округлению его до меньшего целого числа.If is negative, the presence of any fractional component causes it to be rounded to the smaller integer. Операция этого метода отличается от Ceiling метода, который поддерживает округление в сторону положительной бесконечности.The operation of this method differs from the Ceiling method, which supports rounding toward positive infinity.

Начиная с Visual Basic 15,8, производительность преобразования типа «двойное в целое число» оптимизирована, если передать значение, возвращаемое методом, в любую функцию целочисленного преобразованияили если значение Double, возвращаемое, автоматически преобразуется в целое число с параметром Option-on , равным OFF.Starting with Visual Basic 15.8, the performance of Double-to-integer conversion is optimized if you pass the value returned by the method to the any of the integral conversion functions, or if the Double value returned by is automatically converted to an integer with Option Strict set to Off. Эта оптимизация позволяет коду выполняться быстрее — до двух раз быстрее для кода, который выполняет большое количество преобразований в целочисленные типы.This optimization allows code to run faster — up to twice as fast for code that does a large number of conversions to integer types. В следующем примере показаны оптимизированные преобразования:The following example illustrates such optimized conversions:

Итого

Чтобы писать числа с большим количеством нулей:

• Используйте краткую форму записи чисел – , с указанным количеством нулей. Например: это с 6-ю нулями .
• Отрицательное число после приводит к делению числа на 1 с указанным количеством нулей. Например: это ( миллионных).

Для других систем счисления:

• Можно записывать числа сразу в шестнадцатеричной (), восьмеричной () и бинарной () системах счисления
• преобразует строку в целое число в соответствии с указанной системой счисления: .
• представляет число в строковом виде в указанной системе счисления .

Для преобразования значений типа и в число:

Используйте parseInt/parseFloat для «мягкого» преобразования строки в число, данные функции по порядку считывают число из строки до тех пор пока не возникнет ошибка.

Для дробей:

• Используйте округления , , , или .
• Помните, что при работе с дробями происходит потеря точности.

Ещё больше математических функций:

Документация по объекту Math

Библиотека маленькая, но содержит всё самое важное