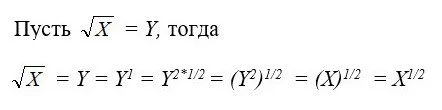Числа в python

Операторы Python

Оператор – это символ или функция, которая выполняет то или иное действие над данными. К примеру, символ + — это оператор сложения.

В Python присутствуют как общие, так и специальные математические операторы.

Ниже приведена таблица наиболее распространённых математических операторов Python.

Операция	Результат
x + y	Сложение (сумма x и y)
x — y	Вычитание (разница между x и y)
-x	Смена знака x
+x	Тождественность x
x * y	Умножение x на y
x / y	Деление x на y
x // y	Получение целой части от деления x на y
x % y	Остаток от деления x / y
x ** y	Возведение в степень

Также руководство охватывает использование операторов присваивания.

Арифметические функции в Python

Арифметические функции используются для представления чисел в различных формах и осуществления над ними математических операций. Далее представлен перечень самых популярных арифметических функций:

• : округление определенного числа вверх;
• : возвращает модуль (абсолютное значение) указанного числа;
• : округление определенного числа вниз;
• : получение наибольшего общего делителя чисел и ;
• : возвращает сумму всех элементов итерируемого объекта;
• : возвращает (e^x)-1;
• : когда значение слишком мало, вычисление может привести к значительной потери в точности. может вернуть вывод с полной точностью.

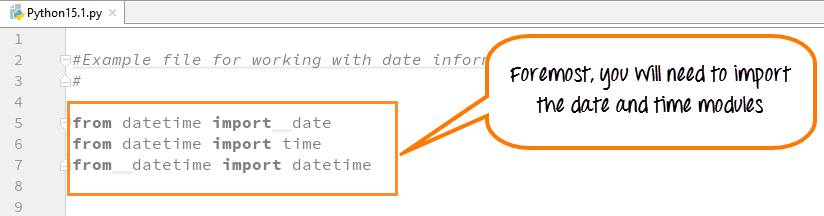
В следующем примере показано использование перечисленных выше функций:

Python

import math

num = -4.28
a = 14
b = 8

num_list =
x = 1e-4 # Малое значение x

print(‘Число:’, num)
print(‘Округление числа вниз:’, math.floor(num))
print(‘Округление числа вверх:’, math.ceil(num))
print(‘Модуль числа:’, math.fabs(num))
print(‘Наибольший общий делитель a и b: ‘ + str(math.gcd(a, b)))
print(‘Сумма элементов списка: ‘ + str(math.fsum(num_list)))
print(‘e^x (при использовании функции exp()) равно:’, math.exp(x)-1)
print(‘e^x (при использовании функции expml()) равно:’, math.expm1(x))

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17

importmath num=-4.28 a=14 b=8 num_list=10,8.25,75,7.04,-86.23,-6.43,8.4 x=1e-4# Малое значение x print(‘Число:’,num) print(‘Округление числа вниз:’,math.floor(num)) print(‘Округление числа вверх:’,math.ceil(num)) print(‘Модуль числа:’,math.fabs(num)) print(‘Наибольший общий делитель a и b: ‘+str(math.gcd(a,b))) print(‘Сумма элементов списка: ‘+str(math.fsum(num_list))) print(‘e^x (при использовании функции exp()) равно:’,math.exp(x)-1) print(‘e^x (при использовании функции expml()) равно:’,math.expm1(x))

Вывод

Python

Число: -4.28
Округление числа вниз: -5
Округление числа вверх: -4
Модуль числа: 4.28
Наибольший общий делитель a и b: 2
Сумма элементов списка: 16.029999999999998
e^x (при использовании функции exp()) равно: 0.0001000050001667141
e^x (при использовании функции expml()) равно: 0.00010000500016667084

1 2 3 4 5 6 7 8

Число-4.28 Округлениечиславниз-5 Округлениечиславверх-4 Модульчисла4.28 Наибольшийобщийделительaиb2 Суммаэлементовсписка16.029999999999998 e^x(прииспользованиифункцииexp())равно0.0001000050001667141 e^x(прииспользованиифункцииexpml())равно0.00010000500016667084

К числу других математических функций относятся:

• : принимает два вещественных аргумента, возводит первый аргумент в степень, значением которой является второй аргумент, после чего возвращает результат. К примеру, эквивалентно выражению ;
• : возвращает квадратный корень определенного числа.

Примеры данных методов представлены ниже:

Возведение в степень

Python

math.pow(3, 4)

1	math.pow(3,4)

Вывод

Shell

81.0

1

81.0

Квадратный корень

Python

math.sqrt(81)

1	math.sqrt(81)

Вывод

Shell

9.0

1

9.0

Операции с числами

Является ли переменная числом

Любую переменную можно проверить на тип (int, float или complex):

Если вы хотите проверить, находится ли в строке число, воспользуйтесь методом

Однако стоит помнить, что метод не работает для отрицательных чисел и чисел с плавающей точкой.

Также для проверки на число, можно написать собственную функцию:

Арифметические операции

• – сложение;
• – вычитание;
• – умножение;
• – деление;
• – целочисленное деление;
• – остаток от деления;
• – возведение в степень;
• – смена знака;
• – модуль числа;
• – возвращает кортеж из частного и остатка от деления x на y;
• – возведение числа в степень (z – деление по модулю);
• – округление числа (ndigits — знаки после запятой).

Преобразования

• – преобразование в целое число
• – преобразование в число с плавающей точкой
• – преобразование в комплексное число
• – целоe числа в двоичную строку;
• – целое число в восьмеричную строку;
• – целое число в шестнадцатеричную строку;
• – перевод целого числа 123 в список цифр этого числа;
• – перевод списка цифр в целое число 123;
• – число в строку;

Ввод чисел

Для ввода данных в программу на языке Python используется функция . Эта функция считывает то что вы ввели на клавиатуре, и записывает эти данные в переменную в виде одной строки. После этого, перевести строку в число можно простыми функциями , или

Если нужен список чисел, введите несколько чисел через пробел и выполните:

Вывод чисел

Для вывода числа используйте

На практике возникают ситуации, когда нужно вывести число вместе со строкой (например пояснить, что означает число). Существует несколько вариантов сделать это:

Другие полезные функции

• – посчитает длину числа;
• – если остаток от деления равен 0, то число четное;
• – диапазон чисел от 0 до 5, по которому можно итерироваться;
• – перевернет число (123 -> 321).

Приоритет

Иногда выражение содержит несколько операторов. В этом случае приоритет оператора используется для определения порядка выполнения.

• Мы можем создать группу выражений, используя круглые скобки. Выражение в скобках сначала вычисляется, прежде чем они смогут участвовать в дальнейших вычислениях.
• Некоторые операторы имеют одинаковый уровень приоритета. В этом случае выражение оценивается слева направо.

В таблице ниже перечислены приоритеты операторов в порядке убывания.

Приоритет
** (экспонента)
~ (Дополнение к единицам)
*, /, //, % (Умножение, Деление, Операторы Модуля)
+, – (Сложение, Вычитание)
<<, >> (операторы сдвига вправо и влево)
& (побитовый AND)
|, ^ (побитовый OR, XOR)
==, !=, >, <, >=, <= (сравнения)
=, +=, -=, *=, /=, //=, %= (присваивания)
is, is not (идентификации)
in, not in (принадлежности)
not, and, or (логические)

Как посчитать сумму введенных чисел?

В команде input() можно передавать подсказки.

w = int(input(«Введите первое число: «)) q = int(input(«Введите второе число: «)) summa=w+q print(summa)

Введите первое число: 6 Введите второе число: 7 13

Копирование материалов разрешается только с указанием автора (Михаил Русаков) и индексируемой прямой ссылкой на сайт (http://myrusakov.ru)!

Добавляйтесь ко мне в друзья : http://vk.com/myrusakov.Если Вы хотите дать оценку мне и моей работе, то напишите её в моей группе: http://vk.com/rusakovmy.

Если Вы не хотите пропустить новые материалы на сайте,то Вы можете подписаться на обновления: Подписаться на обновления

Если у Вас остались какие-либо вопросы, либо у Вас есть желание высказаться по поводу этой статьи, то Вы можете оставить свой комментарий внизу страницы.

Порекомендуйте эту статью друзьям:

Если Вам понравился сайт, то разместите ссылку на него (у себя на сайте, на форуме, в контакте):

Она выглядит вот так:

BB-код ссылки для форумов (например, можете поставить её в подписи):

Арифметические операции

Целые числа поддерживают следующие математические операции, которые отсортированы по убыванию приоритета:

№	Операция	Результат	Замечание
1		возводит x в степень y	(I)
2		возводит x в степень y по модулю z, где z – необязательный аргумент	(I)
3		возвращает кортеж с парой чисел	(II)
4		возвращает \(\bar{x}\) — число, которое комплексно сопряжено с \(x\)
5		преобразует re в комплексное число (по умолчанию )	(VI)
6		преобразует x в вещественное число (число с плавающей точкой)	(VI)
7		переобразует x в целое число, представленное в десятичной системе счисления	(V)(VI)
8		абсолютное значение (модуль) числа x
9		делает число x положительным
10		делает число x отрицательным
11		остаток от деления x на y	(II)
12		результат целочисленного деления x на y	(III) (II)
13		результат «истинного» деления x на y	(IV)
14		произведение x и y
15		разность x и y
16		сумма x и y

Важно: приоритет математических операций выше побитовых логических операций и операций сравнения.

Замечания:

I. возведение \(0\) в степень \(0\) возвращает \(1\):

Извлечение корней четной степени из отрицательных чисел не вызывает ошибки, а возвращает комплексное число:

II. функция и операция , не работают для комплексных чисел. Для вас это может быть и очевидно, но не пользователя для которого вы пишите программу.

III. если оба числа типа int то и результат будет типа int. Данная операция всегда возвращает целое число, т.е. если число x можно представить в виде , то (r – остаток от деления). Так же следует иметь ввиду, что результат данной операции всегда округляется в сторону минус бесконечности:

Это немного сбивает с толку, но проверив результат по формуле , вы убедитесь что все верно.

IV. даже если оба числа типа int, то результат все равно будет преобразован к типу float.

V. встроенная функция пропускает числа (объекты) типа int «как есть», не выполняя над ними, абсолютно никаких действий.

VI. строго говоря эти функции не являются математическими, но они могут учавствовать в математических выражениях Python и поэтому должны обладать приоритетом.

Сложение и вычитание

Операции сложения и вычитания в Python выполняются точно так же, как и в обычной математике. Вы даже можете использовать Python вместо калькулятора.

Например:

Также вы можете объявить переменные и указать их в функции print:

Целые числа бывают положительными и отрицательными. Попробуйте сложить следующие числа:

Числа с плавающей точкой складываются аналогичным образом:

В результате сложения чисел с плавающей точкой также получается число с плавающей точкой, потому Python выводит 8.0, а не 8.

Синтаксис вычитания отличается от сложения только оператором. Попробуйте отнять 32 из 75.67:

Примечание: Если в операции присутствует хотя бы одно число с плавающей точкой, в результате Python также выведет число с плавающей точкой.

Округление десятичного числа

При работе с десятичными числами важно иметь возможность быстро округлить его до N знаков после запятой. Строенная функция round() выполняет эту задачу

При этом ей необходимо два числа: A – число, которое нужно округлить, B – количество знаков после запятой.

Например:

Попробуйте написать простую программу, которая будет подсчитывать чаевые. К примеру, три человека хотят разделить счет в ресторане в $87.93 и оставить 20%  чаевых.

В результате получилось число с большим количеством десятичных знаков. Функция round() округлила его до двух знаков после запятой.

Чтобы округлить десятичное число до целого числа, задайте 0 в качестве второго параметра (в данном случае тип данных не преобразуется, после запятой будет 0):

Функция round() может работать и с целыми числами. Если в качестве первого параметра задано целое число, в результате функция также вернёт целое число.

Конструирование и инициализация.

Это первый метод, который будет вызван при инициализации объекта. Он принимает в качестве параметров класс и потом любые другие аргументы, которые будут переданы в . используется весьма редко, но иногда бывает полезен, в частности, когда класс наследуется от неизменяемого (immutable) типа, такого как кортеж (tuple) или строка. Я не намерен очень детально останавливаться на , так как он не то чтобы очень часто нужен, но этот метод очень хорошо и детально описан в .

Инициализатор класса. Ему передаётся всё, с чем был вызван первоначальный конструктор (так, например, если мы вызываем , получит и в качестве аргументов. почти повсеместно используется при определении классов.

Если и образуют конструктор объекта, это его деструктор. Он не определяет поведение для выражения (поэтому этот код не эквивалентен ). Скорее, он определяет поведение объекта в то время, когда объект попадает в сборщик мусора. Это может быть довольно удобно для объектов, которые могут требовать дополнительных чисток во время удаления, таких как сокеты или файловыве объекты. Однако, нужно быть осторожным, так как нет гарантии, что будет вызван, если объект продолжает жить, когда интерпретатор завершает работу. Поэтому не может служить заменой для хороших программистских практик (всегда завершать соединение, если закончил с ним работать и тому подобное)

Фактически, из-за отсутствия гарантии вызова, не должен использоваться почти никогда; используйте его с осторожностью!Замечание от переводчика: svetlov , что здесь автор ошибается, на самом деле всегда вызывается по завершении работы интерпретатора.

Представление своих классов

Определяет поведение функции , вызванной для экземпляра вашего класса.

Определяет поведение функции , вызыванной для экземпляра вашего класса. Главное отличие от в целевой аудитории. больше предназначен для машинно-ориентированного вывода (более того, это часто должен быть валидный код на Питоне), а предназначен для чтения людьми.

Определяет поведение функции , вызыванной для экземпляра вашего класса. похож на , но возвращает строку в юникоде. Будте осторожны: если клиент вызывает на экземпляре вашего класса, а вы определили только , то это не будет работать. Постарайтесь всегда определять для случая, когда кто-то не имеет такой роскоши как юникод.

Определяет поведение, когда экземпляр вашего класса используется в форматировании строк нового стиля. Например, приведёт к вызову . Это может быть полезно для определения ваших собственных числовых или строковых типов, которым вы можете захотеть предоставить какие-нибудь специальные опции форматирования.

Определяет поведение функции , вызыванной для экземпляра вашего класса. Метод должен возвращать целочисленное значение, которое будет использоваться для быстрого сравнения ключей в словарях. Заметьте, что в таком случае обычно нужно определять и тоже. Руководствуйтесь следующим правилом: подразумевает .

Определяет поведение функции , вызванной для экземпляра вашего класса. Должна вернуть True или False, в зависимости от того, когда вы считаете экземпляр соответствующим True или False.

Определяет поведение функции , вызванной на экземпляре вашего класса. Этот метод должен возвращать пользователю список атрибутов

Обычно, определение не требуется, но может быть жизненно важно для интерактивного использования вашего класса, если вы переопределили или (с которыми вы встретитесь в следующей части), или каким-либо другим образом динамически создаёте атрибуты.

Определяет поведение функции , вызыванной на экземпляре вашего класса. Метод должен вернуть размер вашего объекта в байтах

Он главным образом полезен для классов, определённых в расширениях на C, но всё-равно полезно о нём знать.

Арифметические операции

Целые числа поддерживают следующие математические операции, которые отсортированы по убыванию приоритета:

№	Операция	Результат	Замечание
1		возводит x в степень y	(I)
2		возводит x в степень y по модулю z, где z – необязательный аргумент	(I)
3		возвращает кортеж с парой чисел	(II)
4		возвращает \(\bar{x}\) — число, которое комплексно сопряжено с \(x\)
5		преобразует re в комплексное число (по умолчанию )	(V)
6		преобразует x в вещественное число (число с плавающей точкой)	(V)
7		переобразует x в целое число, представленное в десятичной системе счисления	(V)
8		абсолютное значение (модуль) числа x
9		делает число x положительным
10		делает число x отрицательным
11		остаток от деления x на y	(II)
12		результат целочисленного деления x на y	(III) (II)
13		результат «истинного» деления x на y
14		произведение x и y
15		разность x и y
16		сумма x и y

Важно: приоритет математических операций выше побитовых логических операций и операций сравнения.

Замечания:

I. возведение \(0\) в степень \(0\) возвращает \(1\):

Извлечение корней четной степени из отрицательных чисел не вызывает ошибки, а возвращает комплексное число:

Использование в выражении слишком больших значений x и y типа может привести к ошибке OverflowError.

II. функция и операции , не работают для комплексных чисел. Для вас это может быть и очевидно, но не пользователя для которого вы пишите программу.

III. Данная операция всегда возвращает целое число, т.е. если число x можно представить в виде , то (r – остаток от деления). Так же следует иметь ввиду, что результат данной операции всегда округляется в сторону минус бесконечности:

Это немного сбивает с толку, но проверив результат по формуле , вы убедитесь что все верно.

IV. встроенная функция отбрасывает дробную часть вещественных чисел:

V. строго говоря эти функции не являются математическими, но они могут учавствовать в математических выражениях Python и поэтому должны обладать приоритетом.

Конструирование и инициализация.

Это первый метод, который будет вызван при инициализации объекта. Он принимает в качестве параметров класс и потом любые другие аргументы, которые будут переданы в . используется весьма редко, но иногда бывает полезен, в частности, когда класс наследуется от неизменяемого (immutable) типа, такого как кортеж (tuple) или строка. Я не намерен очень детально останавливаться на , так как он не то чтобы очень часто нужен, но этот метод очень хорошо и детально описан в .

Инициализатор класса. Ему передаётся всё, с чем был вызван первоначальный конструктор (так, например, если мы вызываем , получит и в качестве аргументов. почти повсеместно используется при определении классов.

Если и образуют конструктор объекта, это его деструктор. Он не определяет поведение для выражения (поэтому этот код не эквивалентен ). Скорее, он определяет поведение объекта в то время, когда объект попадает в сборщик мусора. Это может быть довольно удобно для объектов, которые могут требовать дополнительных чисток во время удаления, таких как сокеты или файловыве объекты. Однако, нужно быть осторожным, так как нет гарантии, что будет вызван, если объект продолжает жить, когда интерпретатор завершает работу. Поэтому не может служить заменой для хороших программистских практик (всегда завершать соединение, если закончил с ним работать и тому подобное)

Фактически, из-за отсутствия гарантии вызова, не должен использоваться почти никогда; используйте его с осторожностью!Замечание от переводчика: svetlov , что здесь автор ошибается, на самом деле всегда вызывается по завершении работы интерпретатора.

Вычисления

Вычисления пределов

Для вычисления пределов в SymPy предусмотрен очень простой синтаксис, а именно . Например, если вы хотите вычислить предел функции , где , то надо написать .

sym.limit(sym.sin(x) / x, x, 0) # результат 1

Также можно вычислять пределы, которые стремятся к бесконечности.

sym.limit(x, x, sym.oo) # результат oo
sym.limit(1 / x, x, sym.oo) # результат 0
sym.limit(x ** x, x, 0) # результат 1

Дифференцирование

Для дифференцирования выражений в есть функция . Ниже даны примеры ее работы.

sym.diff(sym.sin(x), x) # результат cos(?)
sym.diff(sym.sin(2 * x), x) # результат 2cos(2?)
sym.diff(sym.tan(x), x)

Проверим результат последней функции при помощи определения производной через предел.

sym.limit((sym.tan(x + y) - sym.tan(x)) / y, y, 0)

Результат тот же.

Также при помощи этой же функции могут быть вычислены производные более высоких порядков. Синтаксис функции будет следующим: . Ниже приведено несколько примеров.

sym.diff(sym.sin(2 * x), x, 1) # результат 2cos(2?)
sym.diff(sym.sin(2 * x), x, 2) # результат −4sin(2?)
sym.diff(sym.sin(2 * x), x, 3) # результат −8cos(2?)

Разложение в ряд

Для разложения выражения в ряд Тейлора используется следующий синтаксис: .

sym.series(sym.cos(x), x)

sym.series(1/sym.cos(x), x)

Интегрирование

В SymPy реализована поддержка определенных и неопределенных интегралов при помощи функции . Интегрировать можно элементарные, трансцендентные и специальные функции. Интегрирование осуществляется с помощью расширенного алгоритма Риша-Нормана. Также используются различные эвристики и шаблоны. Вот примеры интегрирования элементарных функций:

sym.integrate(sym.sin(x), x) # результат −cos(?)
sym.integrate(sym.log(x), x) # результат ?log(?)−?

Также несложно посчитать интеграл и от специальных функций. Возьмем, например, функцию Гаусса:

sym.integrate(sym.exp(-x ** 2) * sym.erf(x), x)

Результат вычисления можете посмотреть сами. Вот примеры вычисления определенных интегралов.

sym.integrate(x**3, (x, -1, 1)) # результат 0
sym.integrate(sym.sin(x), (x, 0, sym.pi / 2)) # результат 1
sym.integrate(sym.cos(x), (x, -sym.pi / 2, sym.pi / 2)) 
# результат 2

Также можно вычислять определенные интегралы с бесконечными пределами интегрирования (несобственные интегралы).

sym.integrate(sym.exp(-x), (x, 0, sym.oo)) # результат 1

Решение уравнений

При помощи можно решать алгебраические уравнения с одной или несколькими переменными. Для этого используется функция .

sym.solveset(x ** 4 - 1, x) # результат {−1,1,−?,?}

Как можно заметить, первое выражение функции приравнивается к и решается относительно . Также возможно решать некоторые уравнения с трансцендентными функциями.

sym.solveset(sym.exp(x) + 1, x) # результат {?(2??+?)|?∈ℤ}

Системы линейных уравнений

способна решать широкий класс полиномиальных уравнений. Также при помощи данной библиотеки можно решать и системы уравнений. При этом переменные, относительно которых должна быть разрешена система, передаются в виде кортежа во втором аргументе функции , которая используется для таких задач.

solution = sym.solve((x + 5 * y - 2, -3 * x + 6 * y - 15), (x, y))
solution, solution # результат (-3, 1) 

Факторизация

Другим мощным методом исследования полиномиальных уравнений является факторизация многочленов (то есть представление многочлена в виде произведения многочленов меньших степеней). Для этого в предусмотрена функция , которая способна производить факторизацию очень широкого класса полиномов.

f = x ** 4 - 3 * x ** 2 + 1
sym.factor(f)

sym.factor(f, modulus=5)

Булевы уравнения

Также в реализована возможность решения булевых уравнений, что по сути означает проверку булевого выражения на истинность. Для этого используется функция .

sym.satisfiable(x & y) # результат {x: True, y: True}

Данный результат говорит нам о том, что выражение будет истинным тогда и только тогда, когда и истинны. Если выражение не может быть истинным ни при каких значениях переменных, то функция вернет результат .

sym.satisfiable(x & ~x) # результат False

Конвертация типов числа в Python

Python может конвертировать начальный тип числа в другой указанный тип. Данный процесс называется «преобразованием». Python может внутренне конвертировать число одного типа в другой, когда в выражении присутствуют смешанные значения. Такой случай продемонстрирован в следующем примере:

Python

3 + 5.1

1

3+5.1

Вывод

Shell

8.1

1

8.1

В вышеприведенном примере целое число 3 было преобразовано в вещественное число 3.0 с плавающей точкой. Результатом сложения также является число с плавающей точкой (или запятой).

Однако иногда вам необходимо явно привести число из одного типа в другой, чтобы удовлетворить требования параметра функции или оператора. Это можно сделать с помощью различных встроенных функций Python.

Например, чтобы преобразовать целое число в число с плавающей точкой, мы должны вызвать функцию , как показано ниже:

Python

a = 12
b = float(a)
print(b)

1 2 3

a=12 b=float(a) print(b)

Вывод

Shell

12.0

1

12.0

Целое число типа было преобразовано в вещественное число типа . также можно конвертировать в следующим образом:

Python

a = 12.65
b = int(a)
print(b)

1 2 3

a=12.65 b=int(a) print(b)

Вывод

Shell

12

1

12

Вещественное число было преобразовано в целое через удаление дробной части и сохранение базового числа

Обратите внимание, что при конвертации значения в подобным образом число будет усекаться, а не округляться вверх

Заключение

Библиотека Math предоставляет функции и константы, которые можно использовать для выполнения арифметических и тригонометрических операций в Python. Библиотека изначально встроена в Python, поэтому дополнительную установку перед использованием делать не требуется. Для получения дополнительной информации можете просмотреть официальную документацию.