Машинное обучение для начинающих: создание нейронных сетей

Что такое нейрон смещения и для чего он нужен?

В нейронных сетях есть ещё один вид нейронов — нейрон смещения. Он отличается от основного вида нейронов тем, что его вход и выход в любом случае равняется единице. При этом входных синапсов такие нейроны не имеют.

Расположение таких нейронов происходит по одному на слой и не более, также они не могут соединяться синапсами друг с другом. Размещать такие нейроны на выходном слое не целесообразно.

Для чего они нужны? Бывают ситуации, в которых нейросеть просто не сможет найти верное решение из-за того, что нужная точка будет находиться вне пределов досягаемости. Именно для этого и нужны такие нейроны, чтобы иметь возможность сместить область определения.

То есть вес синапса меняет изгиб графика функции, тогда как нейрон смещения позволяет осуществить сдвиг по оси координат Х, таким образом, чтобы нейросеть смогла захватить область недоступную ей без сдвига. При этом сдвиг может быть осуществлён как вправо, так и влево. Схематически нейроны сдвига обычно не обозначаются, их вес учитывается по умолчанию при расчёте входного значения.

Также нейроны смещения позволят получить результат в том случае, когда все остальные нейроны выдают 0 в качестве выходного параметра. В этом случае независимо от веса синапса на каждый следующий слой будет передаваться именно это значение.

Наличие нейрона смещения позволит исправить ситуацию и получить иной результат. Целесообразность использования нейронов смещения определяется путём тестирования сети с ними и без них и сравнения результатов.

Но важно помнить, что для достижения результатов мало создать нейронную сеть. Её нужно ещё и обучить, что тоже требует особых подходов и имеет свои алгоритмы

Этот процесс сложно назвать простым, так как его реализация требует определённых знаний и усилий.

ООО «Нейронные Технологии»

Нейрокомпьютинг и его применение в экономике и бизнесе.

В каждой предметной области при ближайшем рассмотрении можно найти постановки задач для нейронных сетей. Вот список отдельных областей, где решение такого рода задач имеет практическое значение уже сейчас.

Обилие приведенных выше областей применения нейронных сетей — не рекламный трюк. Просто нейросети — это гибкий и мощный набор инструментов решения разнообразных задач обработки и анализа данных.

У Вас есть подобные задачи? Давайте обсудим по электронной почте tsar@neuropro.ru возможности их решения.

далее: нейронные сети — как и где использовать.

Многослойный перцептрон с сигмоидной функцией активации (итерация модели 2)

слойдругого

Пример 1: распознавание паттерна лестницы

1. Построим модель, которая срабатывает при распознавании «левых лестниц», $inline$\widehat y_{left}$inline$
2. Построим модель, которая срабатывает при распознавании «правых лестниц», $inline$\widehat y_{right}$inline$
3. Добавим базовым моделям оценку, чтобы конечная сигмоида срабатывала только если оба значения ($inline$\widehat y_{left}$inline$, $inline$\widehat y_{right}$inline$) велики

Другой вариант

1. Построим модель, срабатывающую, когда нижний ряд тёмный, $inline$\widehat y_1$inline$
2. Построим модель, срабатывающую, когда верхний левый пиксель тёмный и верхний правый пиксель светлый, $inline$\widehat y_2$inline$
3. Построим модель, срабатывающую, когда верхний левый пиксель светлый и верхний правый пиксель тёмный, $inline$\widehat y_3$inline$
4. Добавим базовые модели так, что конечная сигмоидная функция срабатывала только когда $inline$\widehat y_1$inline$и $inline$\widehat y_2$inline$ велики, или когда $inline$\widehat y_1$inline$и $inline$\widehat y_3$inline$ велики. (Заметьте, что $inline$\widehat y_2$inline$ и $inline$\widehat y_3$inline$ не могут быть большими одновременно.)

Пример 2: распознать лестницы светлого оттенка

1. Построим модели, срабатывающие при «затенённом нижнем ряде», «затенённом x1 и белом x2», «затенённом x2 и белом x1», $inline$\widehat y_1$inline$, $inline$\widehat y_2$inline$ и $inline$\widehat y_3$inline$
2. Построим модели, срабатывающие при «тёмном нижнем ряде», «тёмном x1 и белом x2», «тёмном x2 и белом x», $inline$\widehat y_4$inline$, $inline$\widehat y_5$inline$ и $inline$\widehat y_6$inline$
3. Соединим модели таким образом, чтобы «тёмные» идентификаторы вычитались из «затенённых» идентификаторов перед сжиманием результата сигмоидой

Одноодин выходной слойдвутри

Однослойный перцептрон с сигмоидной функцией активации (итерация модели 1)

функция «сигмоида»

$$display$$sigmoid(z) = \frac{1}{1 + e^{-z}}$$display$$

$$display$$z = w \cdot x = w_1x_1 + w_2x_2 + w_3x_3 + w_4x_4$$display$$

$$display$$\widehat y = sigmoid(z) = \frac{1}{1 + e^{-z}}$$display$$

логистическая регрессия$inline$\hat{y}$inline$вероятность

$$display$$f(x)={\begin{cases} 1 &{\text{if }}\ \widehat{y} > 0.5\\ 0 & {\text{otherwise}} \end{cases}} $$display$$

$$display$$\begin{bmatrix} w_1 & w_2 & w_3 & w_4 \end{bmatrix} = \begin{bmatrix} -0.140 & -0.145 & 0.121 & 0.092 \end{bmatrix}$$display$$

$$display$$b = -0.008$$display$$

$$display$$\widehat y = \frac{1}{1 + e^{-(-0.140x_1 -0.145x_2 + 0.121x_3 + 0.092x_4 -0.008)}}$$display$$

Случай B

$inline$x_3$inline$
случай A$inline$z = w \cdot x$inline$$inline$z$inline$случай Aслучай B

1. $inline$\widehat y$inline$ имеет монотонную связь с каждой переменной. А что если нам нужно распознавать лестницы более светлого оттенка?
2. Модель не учитывает взаимодействие переменных. Предположим, что нижний ряд изображения чёрный. Если верхний левый пиксель белый, то затемнение верхнего правого пикселя должно увеличить вероятность паттерна лестницы. Если верхний левый пиксель чёрный, то затенение верхнего правого пикселя должно снижать вероятность лестницы. Другими словами, увеличение $inline$x_3$inline$ должно потенциально приводить к увеличению или уменьшению $inline$\widehat y$inline$, в зависимости от значений других переменных. В нашей текущей модели этого никак не достичь.

Нейронные сети

Нейронная сеть представляет собой вычислительную модель (способ описания системы с использованием математического языка и его принципов). Эта система скорее самообучающаяся и натренированная, нежели явно запрограммированная.

Нейронные сети имитируют центральную нервную систему человека. У них есть соединенные узлы, которые похожи на наши нейроны:

Нейронная сеть

Первым нейронным сетевым алгоритмом был перцептрон

Его внутреннюю работу хорошо раскрывает данная статья (обратите внимание на анимации)

Чтобы понять, как работают нейронные сети, построим архитектуру одной из них с помощью TensorFlow. Можете взглянуть на пример такой реализации.

Архитектура нейронной сети

У нашей нейронной сети будет 2 скрытых слоя (надо выбрать, сколько их будет в вашей модели — это часть проектирования архитектуры). Задача каждого скрытого уровня заключается в том, чтобы превратить входные данные во что-то, что мог бы использовать слой вывода.

Первый скрытый слой

Слой ввода и первый скрытый слой

Вам также надо определить, сколько узлов будет содержать первый скрытый слой. Они называются признаками или нейронами, на изображении сверху каждый представлен синим кругом.

В слое ввода один узел соответствует слову из набора данных. Рассмотрим это чуть позже.

Как объяснено в этой статье, каждый узел (нейрон) умножается на вес, т.е. имеет значение веса. В ходе обучения нейронная сеть регулирует эти показатели, чтобы произвести правильные выходные данные. Сеть также добавляет смещение.

Далее в нашей архитектуре данные передаются функции активации, которая определяет окончательный вывод каждого узла. Приведем аналогию: представьте, что каждый узел — это лампа, а функция активации указывает, будет лампа гореть или нет.

Существует много видов функции активации. Используем усеченное линейное преобразование (ReLu). Эта функция определяется следующим образом:

Примеры: если x = −1, то  (ноль); если x = 0,7, то .

Второй скрытый слой

Второй скрытый слой делает то же самое, что и первый, но теперь входными данными являются выходные данные первого слоя:

Первый и второй скрытые слои

Слой вывода

И, наконец, мы добираемся до последнего пункта — слоя вывода. Чтобы получить его результаты, будем использовать унитарное кодирование. Здесь только один бит равен единице, а все остальные — нулевые. Например, мы хотим закодировать три категории: «спорт», «космос» и «компьютерная графика»:

Получим, что число узлов вывода равно числу классов входного набора данных.

Значения слоя вывода умножаются на веса, к ним добавляется смещение, но функция активации уже другая.

Мы хотим пометить каждый текст категорией, между собой они являются взаимоисключающими, т.к. текст не может принадлежать двум категориям одновременно. Чтобы достичь цели, вместо ReLu возьмем функцию Softmax. Она преобразует вывод для каждой категории в значение между 0 и 1, а также проверяет, что сумма всех значений равна 1. Так вывод покажет нам вероятность принадлежности текста к каждой категории:

Теперь у нас есть граф потока данных нейронной сети. Если перевести все в код, то получится примерно следующее:

Байесовские сети (БС)

Эти графические структуры для представления вероятностных отношений между набором случайных переменных.

В этих сетях каждый узел представляет собой случайную переменную с конкретными предложениями. Например, в медицинской диагностике, узел Рак представляет собой предложение, что пациент имеет рак.

Ребра, соединяющие узлы представляют собой вероятностные зависимости между этими случайными величинами. Если из двух узлов, один влияет на другой узел, то они должны быть связаны напрямую. Сила связи между переменными количественно определяется вероятностью, которая связан с каждым узлом.

Есть только ограничение на дугах в БН, вы не можете вернуться обратно к узле просто следуя по направлению дуги. Отсюда БНС называют ациклическим графом.

Структура БН идеально подходит для объединения знаний и наблюдаемых данных. БН могут быть использованы, чтобы узнать причинно-следственные связи и понимать различные проблемы и предсказывать будущее, даже в случае отсутствия данных.

Нейросети: что это такое и как работает

В идеале, загрузив первичные данные и сопоставив топологию классов, нейросеть далее уже сама сможет классифицировать новую информацию. Допустим, мы решили загрузить изображение 3х5 пикселей. Простая арифметика нам подскажет, что входов будет: 3*5=15. А сама классификация определит общее количество выходов, т.е. нейронов. Другой пример: нейросети необходимо распознать букву “С”. Заданный порог – полное соответствие букве, для этого потребуется один нейрон с количеством входов, равных размеру изображения.

Допустим, что размер будет тот же 3х5 пикселей. Скармливая программе различные картинки букв или цифр, будем учить её определять изображение нужного нам символа.

Как и в любом обучении, ученика за неправильный ответ нужно наказывать, а за верный мы ничего давать не будем. Если верный ответ программа воспринимает как False, то увеличиваем вес входа на каждом синапсе. Если же, наоборот, при неверном результате программа считает результат положительным или True, то вычитаем вес из каждого входа в нейрон. Начать обучение логичнее со знакомства с нужным нам символом. Первый результат будет неверным, однако немного подкорректировав код, при дальнейшей работе программа будет работать корректно. Приведенный пример алгоритма построения кода для нейронной сети называется парцетроном.

Бывают и более сложные варианты работы нейросетей с возвратом неверных данных, их анализом и логическими выводами самой сети. Например, онлайн-предсказатель будущего вполне себе запрограммированная нейросеть. Такие проги способны обучаться как с учителем, так и без него, и носят название адаптивного резонанса. Их суть заключается в том, что у нейронов уже есть свои представления об ожидании о том, какую именно информацию они хотят получить и в каком виде. Между ожиданием и реальностью проходит тонкий порог так называемой бдительности нейронов, которая и помогает сети правильно классифицировать поступающую информацию и не упускать ни пикселя. Фишка АР нейросети в том, что учится она самостоятельно с самого начала, самостоятельно определяет порог бдительности нейронов. Что, в свою очередь, играет роль при классифицировании информации: чем бдительнее сеть, тем она дотошнее.

Самые азы знаний о том, что такое нейросети, мы получили. Теперь попробуем обобщить полученную информацию. Итак, нейросети – это электронный прототип мышлению человека. Они состоят из электронных нейронов и синапсов – потоков информации на входе и выходе из нейрона. Программируются нейросети по принципу обучения с учителем (программистом, который закачивает первичную информацию) или же самостоятельно (основываясь на предположения и ожидания от полученную информацию, которую определяет всё тот же программист). С помощью нейросети можно создать любую систему: от простого определения рисунка на пиксельных изображениях до психодиагностики и экономической аналитики.

Пример 2

Предположим что у Вы являетесь психологом в учебном заведении и перед Вами поставили цель: выявить эмоциональное состояние учащихся. Казалось бы спросить «Какое у тебя сегодня настроение?» дело совершенно плёвое, но когда это необходимо сделать 30 000 раз каждый день(именно столько учащихся Вам необходимо опросить) — это уже становится проблемой.

Предположим что в учебном заведении есть закрытая социальная сеть, в которой учащиеся ежедневно оставляют более 500 000 сообщений. Эта информация строго конфиденциальная, но Вы имеете к ней доступ, так как подписали договор о не разглашении. Отлично! Теперь у нас есть несколько миллионов сообщений вместо 30 000 учеников! 

Эмм… Звучит не особо оптимистично, но помимо психологии Вы увлекаетесь построением ИНС. Действительно. Зачем заниматься классификацией сообщений самому, если это может сделать машина и дать Вам отчет.

Перед нами стоит следующая задача:  Построить ИИС которая будет определять эмоциональное состояние человека по сообщению.

Входными данными является сообщение пользователя.

Выходными данными является строка: «хорошее» — если эмоциональный окрас сообщения позитивный, «плохое» — если эмоциональный окрас сообщения агрессивный или депрессивный.

Пример работы:

Сообщение «Завтра будет просто ужасный день!»

Результат «плохое»

Погрешность конечно оставляет желать лучшего, после 1000 итераций она составляет около 0.011. Это довольно большая цифра если мы говорим о классификации. Если увеличить количество обучающего материала и увеличить количество итераций, то можно добиться более внушительных результатов, но это займет слишком много времени в рамках чтения этой статьи.

Советую сохранять результаты обучения и не заставлять сеть учиться каждый раз когда Вы ее запускаете. Сохранить результаты обучения сети можно при помощи функции . Далее полученную строку сохраните в файл и при последующем запуске при помощи команды выгрузите результаты вычислений обратно в сеть.

В работе ИНС всегда будут присутствовать ошибки, тем более на первых порах. Ведь ИНС подобно ребенку, в раннем возрасте ей свойственно часто ошибаться. Чем больше тренировок и качественнее будет обучающий материал, тем более точными будут результаты работы ИНС.

В заключение хочу сказать что JavaScript безусловно не является языком наиболее подходящим для построения ИНС. Вы наверно уже заметили как медленно проходит процесс обучения. Это вызвано тем что NodeJS, как и JavaScript является однопоточным и не раскрывает все вычислительные возможности процессора. Разработчики brain.js обещают улучшить производительность с выходом 2-й версии. Хотя и сейчас есть возможность использовать мощность видеопроцессора при помощи WebGL, но работу через GPU в brain.js поддерживают только neural networks. Для дальнейшего изучения рекомендую посмотреть в сторону Python.

1. Основы ИНС

2. https://habr.com/company/epam_systems/blog/317050/
3. https://habr.com/post/312450/
4. https://habr.com/post/40137/
5. https://habr.com/post/398645/
6. https://tproger.ru/translations/javascript-brain-neural-framework/
7. https://itnan.ru/post.php?c=1&p=304414
8. https://habr.com/post/183462/
9. https://medium.com/openmindonline/emotion-detection-with-javascript-neural-networks-5a408f84eb75

Что такое нейронные сети и их типы?

Первый вопрос, который возникает у интересующихся, что же такое нейронная сеть? В классическом определении это определённая последовательность нейронов, которые объединены между собой синапсами. Нейронные сети являются упрощённой моделью биологических аналогов.

Программа, имеющая структуру нейронной сети, даёт возможность машине анализировать входные данные и запоминать результат, полученный из определённых исходников. В последующем подобный подход позволяет извлечь из памяти результат, соответствующий текущему набору данных, если он уже имелся в опыте циклов сети.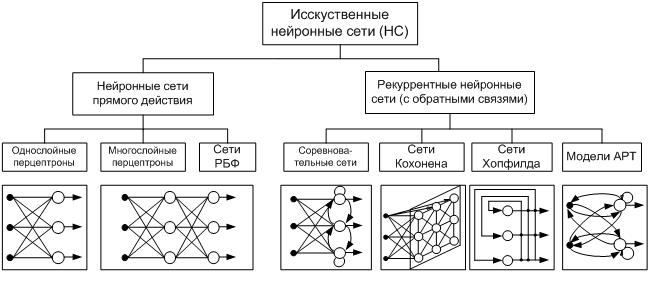

Многие воспринимают нейронную сеть, как аналог человеческого мозга. С одной стороны, можно считать это суждение близким к истине, но, с другой стороны, человеческий мозг слишком сложный механизм, чтобы была возможность воссоздать его с помощью машины хотя бы на долю процента. Нейронная сеть — это в первую очередь программа, основанная на принципе действия головного мозга, но никак не его аналог.

Нейронная сеть представляет собой связку нейронов, каждый из которых получает информацию, обрабатывает её и передаёт другому нейрону. Каждый нейрон обрабатывает сигнал совершенно одинаково.

Как тогда получается различный результат? Все дело в синапсах, которые соединяют нейроны друг с другом. Один нейрон может иметь огромное количество синапсов, усиливающих или ослабляющих сигнал, при этом они имеют особенность изменять свои характеристики с течением времени.

Определившись в общих чертах, что собой представляет нейронная сеть, можно выделить основные типы их классификации. Прежде чем приступить к классификации необходимо ввести одно уточнение. Каждая сеть имеет первый слой нейронов, который называется входным.

Он не выполняет никаких вычислений и преобразований, его задача состоит только в одном: принять и распределить по остальным нейронам входные сигналы. Это единственный слой, который является общим для всех типов нейронных сетей, дальнейшая их структура и является критерием для основного деления.

• Однослойная нейронная сеть. Это структура взаимодействия нейронов, при которой после попадания входных данных в первый входной слой сразу передаётся в слой выхода конечного результата. При этом первый входной слой не считается, так как он не выполняет никаких действий, кроме приёма и распределения, об этом уже было сказано выше. А второй слой производит все нужные вычисления и обработки и сразу выдаёт конечный результат. Входные нейроны объединены с основным слоем синапсами, имеющими различный весовой коэффициент, обеспечивающий качество связей.
• Многослойная нейронная сеть. Как понятно из определения, этот вид нейронных сетей помимо входного и выходного слоёв имеет ещё и промежуточные слои. Их количество зависит от степени сложности самой сети. Она в большей степени напоминает структуру биологической нейронной сети. Такие виды сетей были разработаны совсем недавно, до этого все процессы были реализованы с помощью однослойных сетей. Соответственно подобное решение имеет намного больше возможностей, чем её предок. В процессе обработки информации каждый промежуточный слой представляет собой промежуточный этап обработки и распределения информации.

В зависимости от направления распределения информации по синапсам от одного нейрона к другому, можно также классифицировать сети на две категории.

• Сети прямого распространения или однонаправленная, то есть структура, в которой сигнал движется строго от входного слоя к выходному. Движение сигнала в обратном направлении невозможно. Подобные разработки достаточно широко распространены и в настоящий момент с успехом решают такие задачи, как распознавание, прогнозы или кластеризация.
• Сети с обратными связями или рекуррентная. Подобные сети позволяют сигналу двигаться не только в прямом, но и в обратном направлении. Что это даёт? В таких сетях результат выхода может возвращаться на вход исходя из этого, выход нейрона определяется весами и сигналами входа, и дополняется предыдущими выходами, которые снова вернулись на вход. Таким сетям свойственна функция кратковременной памяти, на основании которой сигналы восстанавливаются и дополняются в процессе обработки.

Это не единственные варианты классификации сетей.

Упрощение

В прошлой главе я постоянно говорил о каких-то серьезных упрощениях. Причина упрощений заключается в том, что никакие современные компьютеры не могут быстро моделировать такие сложные системы, как наш мозг. К тому же, как я уже говорил, наш мозг переполнен различными биологическими механизмами, не относящиеся к обработке информации.

Нам нужна модель преобразования входного сигнала в нужный нам выходной. Все остальное нас не волнует. Начинаем упрощать.

Биологическая структура → схема

В предыдущей главе вы поняли, насколько сложно устроены биологические нейронные сети и биологические нейроны. Вместо изображения нейронов в виде чудовищ с щупальцами давайте просто будем рисовать схемы.

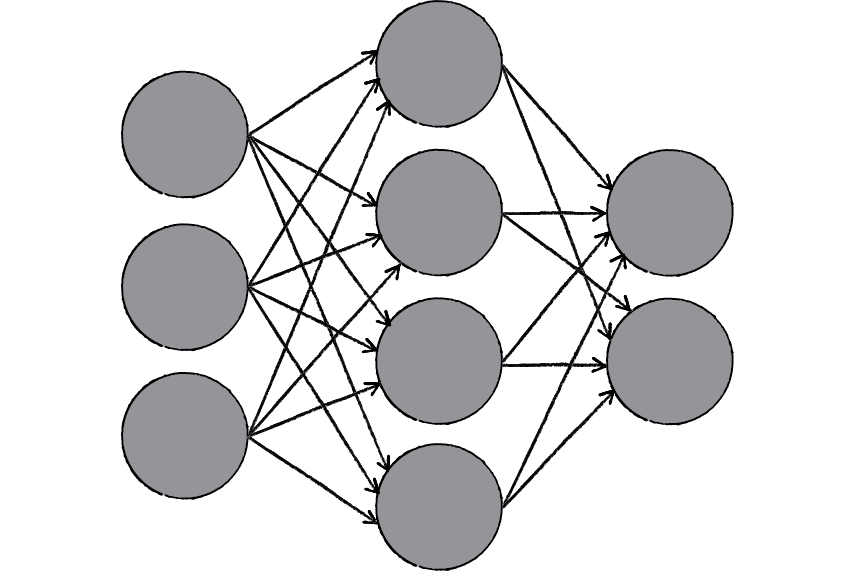
Вообще говоря, есть несколько способов графического изображения нейронных сетей и нейронов. Здесь мы будем изображать искусственные нейроны в виде кружков.

Вместо сложного переплетения входов и выходов будем использовать стрелки, обозначающие направление движения сигнала.

Таким образом искусственная нейронная сеть может быть представлена в виде совокупности кружков (искусственных нейронов), связанных стрелками.

Электрические сигналы → числа

В реальной биологической нейронной сети от входов сети к выходам передается электрический сигнал. В процессе прохода по нейронной сети он может изменяться.

Электрический сигнал всегда будет электрическим сигналом. Концептуально ничего не изменяется. Но что же тогда меняется? Меняется величина этого электрического сигнала (сильнее/слабее). А любую величину всегда можно выразить числом (больше/меньше).

В нашей модели искусственной нейронной сети нам совершенно не нужно реализовывать поведение электрического сигнала, так как от его реализации все равно ничего зависеть не будет.

На входы сети мы будем подавать какие-то числа, символизирующие величины электрического сигнала, если бы он был. Эти числа будут продвигаться по сети и каким-то образом меняться. На выходе сети мы получим какое-то результирующее число, являющееся откликом сети.

Для удобства все равно будем называть наши числа, циркулирующие в сети, сигналами.

Синапсы → веса связей

Вспомним картинку из первой главы, на которой цветом были изображены связи между нейронами – синапсы. Синапсы могут усиливать или ослаблять проходящий по ним электрический сигнал.

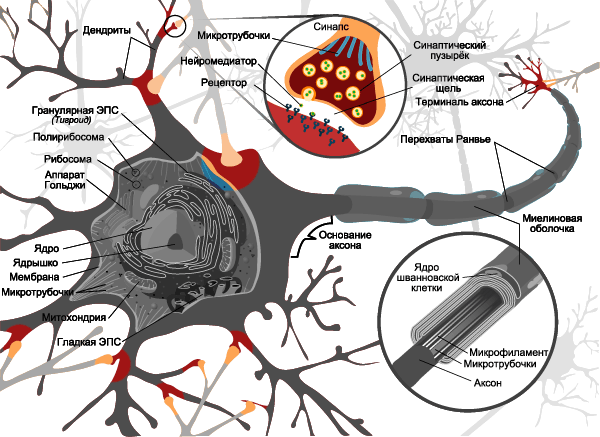
Давайте характеризовать каждую такую связь определенным числом, называемым весом данной связи. Сигнал, прошедший через данную связь, умножается на вес соответствующей связи.

Это ключевой момент в концепции искусственных нейронных сетей, я объясню его подробнее. Посмотрите на картинку ниже. Теперь каждой черной стрелке (связи) на этой картинке соответствует некоторое число ​\( w_i \)​ (вес связи). И когда сигнал проходит по этой связи, его величина умножается на вес этой связи.

На приведенном выше рисунке вес стоит не у каждой связи лишь потому, что там нет места для обозначений. В реальности у каждой ​\( i \)​-ой связи свой собственный ​\( w_i \)​-ый вес.

Математика. Часть 2 (сложная)

Функция ошибки

$inline$y_{true}$inline$

$$display$$NN(picture | \Omega) = y_{pred}$$display$$

$$display$$p(y_{pred} = y_{true} | \Omega)$$display$$

$$display$$NN(picture | \Omega) = \left$$display$$

$$display$$p(y_{pred} = y_{true} | \Omega) = p_\Omega (y_{pred})^t_{0} * (1 — p_\Omega (y_{pred}))^t_{1} = \\ p_0^{t_0} * p_1^{t_1}$$display$$

$inline$t_0, t_1$inline$$inline$y_{true} = cat$inline$$inline$t_0 == 1, t_1 == 0$inline$$inline$y_{true} = dog$inline$$inline$t_0 == 0, t_1 == 1$inline$

$$display$$p(y_{pred} = y_{true} | \Omega) = \prod_0 ^m p_i^{t_i}$$display$$

$$display$$MaximumLikelyhood = \prod_{j=0} ^N \prod_{i=0} ^m p_{i,j}^{t_{i,j}}$$display$$

$$display$$CrossEntropyLoss = — \sum\limits_{j=0}^{N} \sum\limits_{i=0}^{m}t_{i,j}\cdot\log(p_{i,j})$$display$$

$$display$$\frac{\partial CrossEntropyLoss}{\partial p_j} = — \frac{\boldsymbol{t_j}}{\boldsymbol{p_{j}}}$$display$$

$inline$t_{i,j} \neq 0$inline$

Функции активации

Softmax

$$display$$Softmax_i = \frac{e^{x_i}}{\sum \limits_{j} e^{x_j}}$$display$$

$inline$\boldsymbol{x}$inline$

$$display$$J_{Softmax} = \begin{cases} x_i — x_i \cdot x_j, i = j\\ — x_i \cdot x_j, i \neq j \end{cases}$$display$$

$inline$\boldsymbol{dz}$inline$$inline$\boldsymbol{dz}$inline$$inline$\boldsymbol{dz}$inline$$inline$\boldsymbol{dz_{new}}$inline$$inline$\boldsymbol{dz}$inline$$inline$J_{Softmax}$inline$

$$display$$dz_{new} = \boldsymbol{dz} \times J_{Softmax}$$display$$

$inline$\boldsymbol{dz_{new}}$inline$

ReLU

$$display$$ReLU(x) = \begin{cases} x, x > 0\\ 0, x < 0 \end{cases}$$display$$

$$display$$d(ReLU(x)) = \begin{cases} 1, x > 0\\ 0, x < 0 \end{cases}$$display$$

Полносвязный слой

$$display$$W = |w_{i,j}|$$display$$

$$display$$\boldsymbol{x}_{new} = W\cdot \boldsymbol{x}$$display$$

$inline$\boldsymbol{x}$inline$$inline$input\_shape$inline$$inline$x_{new}$inline$$inline$output\_shape$inline$$inline$\boldsymbol{x}$inline$$inline$\boldsymbol{x}_{new}$inline$$inline$w_{1,1}$inline$$inline$\boldsymbol{x}_{new}$inline$$inline$x_{new~1} = w_{1,1} \cdot x_1 + … + w_{1,784} \cdot x_{784} $inline$$inline$x_{new~1}$inline$$inline$w_{1,1}$inline$$inline$x_1$inline$$inline$d\boldsymbol{z} $inline$$inline$dz_1 $inline$$inline$x_{new~1}$inline$$inline$x_1, x_2, … , x_{784}$inline$

$$display$$\frac{\partial L}{\partial W} = (d\boldsymbol{z},~dW) = \left( \begin{matrix} dz_{1} \cdot \boldsymbol{x} \\ … \\ dz_{100} \cdot\boldsymbol{x} \end{matrix}\right)_{100}$$display$$

$inline$\frac{\partial L}{\partial W}$inline$$inline$d\boldsymbol{z}$inline$

$$display$$\frac{\partial L}{\partial W} = d\boldsymbol{z} \cdot \frac{\partial \boldsymbol{x}_{new}(W)}{\partial W}$$display$$

$inline$\boldsymbol{x}_{new}$inline$$inline$\boldsymbol{x}_{new} = W\cdot \boldsymbol{x}$inline$

$$display$$\frac{\partial L}{\partial W} = d\boldsymbol{z} \cdot \frac{\partial W\cdot \boldsymbol{x}}{\partial W} = d\boldsymbol{z} \cdot E \cdot \boldsymbol{x}$$display$$

$inline$\boldsymbol{x}$inline$$inline$\boldsymbol{x}(W_{old})$inline$

$$display$$\begin{gathered} \frac{\partial L}{\partial W_{old}} = d\boldsymbol{z} \cdot \frac{\partial \boldsymbol{x}_{new}(W)}{\partial W_{old}} = d\boldsymbol{z} \cdot \frac{\partial W\cdot \boldsymbol{x}(W_{old})}{\partial W_{old}} = \\ = d\boldsymbol{z} \cdot \frac{\partial W\cdot W_{old}\cdot\boldsymbol{x}_{old}}{\partial W_{old}} = d\boldsymbol{z} \cdot W \cdot E \cdot \boldsymbol{x}_{old} = \\ = d\boldsymbol{z}_{new} \cdot E \cdot \boldsymbol{x}_{old} \end{gathered}$$display$$

$inline$d\boldsymbol{z}_{new} = d\boldsymbol{z} \cdot W$inline$

Однослойный перцептрон (итерация модели 0)

перцептрона

$$display$$f(x)={\begin{cases} 1 &{\text{if }}\ w_1x_1 + w_2x_2 + w_3x_3 + w_4x_4 > threshold\\ 0 & {\text{otherwise}} \end{cases}}$$display$$

$$display$$\widehat y = \mathbf w \cdot \mathbf x + b$$display$$

$$display$$f(x)={\begin{cases} 1 &{\text{if }}\ \widehat{y} > 0\\ 0 & {\text{otherwise}} \end{cases}}$$display$$

$inline$\hat{y}$inline$оценка прогноза

$$display$$\hat{y}=-0.0019x_{1}+0.0016x_{2}+0.0020x_{3}+0.0023x_{4}+0.0003$$display$$

$inline$x_{3}$inline$$inline$x_{4}$inline$

1. Модель выдаёт на выходе действительное число, значение которого коррелирует с концепцией похожести (чем больше значение, тем выше вероятность того, что на изображении есть лестница), но нет никакой основы для интерпретации этих значений как вероятностей, потому что они могут находиться вне интервала .
2. Модель не может ухватить нелинейные взаимосвязи между переменными и целевым значением. Чтобы убедиться в этом, рассмотрим следующие гипотетические сценарии:

Случай B

$inline$x_{3}$inline$
случай A$inline$\hat{y}$inline$случай B$inline$x_{3}$inline$$inline$\hat{y}$inline$