Merge sort algorithm

Сортировка Слиянием (Merge-Sort)

Подробности

Категория: Сортировка и поиск

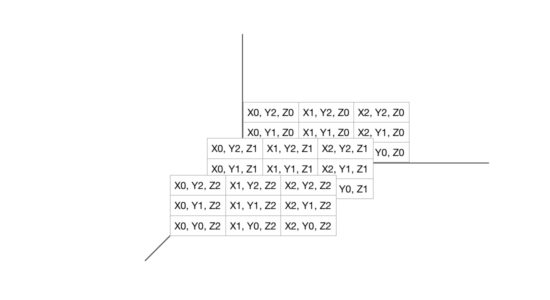
Сортировка слиянием (англ. merge sort) — алгоритм сортировки, который упорядочивает списки (или другие структуры данных, доступ к элементам которых можно получать только последовательно, например — потоки) в определённом порядке. Эта сортировка — хороший пример использования принципа «разделяй и властвуй». Сначала задача разбивается на несколько подзадач меньшего размера. Затем эти задачи решаются с помощью рекурсивного вызова или непосредственно, если их размер достаточно мал. Наконец, их решения комбинируются, и получается решение исходной задачи.

1. массив рекурсивно разбивается пополам, и каждая из половин делиться до тех пор, пока размер очередного подмассива не станет равным единице;
2. далее выполняется операция алгоритма, называемая слиянием. Два единичных массива сливаются в общий результирующий массив, при этом из каждого выбирается меньший элемент (сортировка по возрастанию) и записывается в свободную левую ячейку результирующего массива. После чего из двух результирующих массивов собирается третий общий отсортированный массив, и так далее. В случае если один из массивов закончиться, элементы другого дописываются в собираемый массив;
3. в конце операции слияния, элементы перезаписываются из результирующего массива в исходный.

Худшее время	O(n log n)
Лучшее время	O(n log n) обычно, O(n) на упорядоченном массиве
Среднее время	O(n log n)
Затраты памяти	O(n) вспомогательных

Реализация алгоритма на различных языках программирования:

Writing the Code for Merge Algorithm

A noticeable difference between the merging step we described above and the one we use for merge sort is that we only perform the merge function on consecutive sub-arrays.

This is why we only need the array, the first position, the last index of the first subarray(we can calculate the first index of the second subarray) and the last index of the second subarray.

Our task is to merge two subarrays A and A to create a sorted array A. So the inputs to the function are A, p, q and r

The merge function works as follows:

1. Create copies of the subarrays and M ← A.
2. Create three pointers i, j and k
   1. i maintains current index of L, starting at 1
   2. j maintains current index of M, starting at 1
   3. k maintains the current index of A, starting at p.
3. Until we reach the end of either L or M, pick the larger among the elements from L and M and place them in the correct position at A
4. When we run out of elements in either L or M, pick up the remaining elements and put in A

In code, this would look like:

Быстрая сортировка (Quick Sort)

Этот широко известный алгоритм сортировки был разработан английским информатиком Чарльзом Хоаром во время его работы в МГУ в советские годы.

Один из самых быстрых известных универсальных алгоритмов сортировки массивов: в среднем O(n log n) обменов при упорядочении n-элементов; из-за наличия ряда недостатков на практике обычно используется с некоторыми доработками.

Быстрая сортировка относится к алгоритмам «разделяй и властвуй».

Алгоритм состоит из трёх шагов:

1. Выбор опорного элемента из массива.
2. Перераспределение элементов в массиве таким образом, что элементы меньше опорного помещаются перед ним, а больше или равные — после.
3. Рекурсивное применение первых двух шагов к двум подмассивам слева и справа от опорного элемента. Рекурсия не применяется к массиву, в котором только один или отсутствуют элементы.

С исходным кодом алгоритма и его интерактивной презентацией вы сможете ознакомиться на специальном ресурсе.

TurboBasic 1.1

CLS
RANDOMIZE TIMER
DEFINT X, Y, N, I, J, D
N = 10 ' 32 766 - 62.7 SEC
DIM Y, Y1, Y2, Y3, Y4 'FRE(-1)=21440-21456
 
PRINT " ZAPOLNENIE MASSIVA ELEMENTAMI"
 
FOR X = 1 TO N
   Y = X
   PRINT Y;
NEXT X:PRINT
 
PRINT " PEREMESHIVANIJE ELEMENTOV MASSIVA"
 
PRINT " SLUCHAINYE CHISLA"
 
FOR X = 1 TO N
   YD=Y
   XS=INT(RND*N)+1
   PRINT XS;
   Y=Y
   Y=YD
NEXT X:PRINT
 
PRINT " PEREMESHANNYJ MASSIV"
 
FOR X=1 TO N
   PRINT Y;
NEXT X:PRINT
 
'ALGORITM "SORTIROVKA VYBOROM" O(N^2)
 
L=1
R=N
MTIMER
FOR J=1 TO R-1 STEP 1
   MIN=J
   FOR I=J+1 TO R STEP 1
      IF Y < Y THEN MIN=I
   NEXT I
   IF MIN<>J THEN SWAP Y,Y
 
   LOCATE 7,1                            REM
   FOR I=1 TO N:PRINT Y;:NEXT I:PRINT REM ANIMATION BLOCK
   DELAY 1                               REM
 
NEXT J
T1=MTIMER
 
PRINT " OTSORTIROVANNYJ MASSIV"
 
FOR X=1 TO N
   'PRINT "Y=";Y
   PRINT Y;
NEXT X:PRINT
PRINT "ELAPSED TIME=";T1
PRINT FRE(-1)

Сортировка выбором проста в реализации, и в некоторых ситуациях стоит предпочесть ее наиболее сложным и совершенным методам. Но в большинстве случаев данный алгоритм уступает в эффективности последним, так как в худшем, лучшем и среднем случае ей потребуется О(n2) времени. 

При написании статьи были использованы открытые источники сети интернет :

Youtube

Delphi (сортировка произвольных типов данных — простое слияние)[править]

unit uMergeSort;

interface
type
  TItem = Integer;               //Здесь можно написать Ваш произвольный тип
  TArray = array of TItem;

  procedure MergeSort(var Arr TArray);

implementation

function IsBigger(d1, d2  TItem)  Boolean;
begin
  Result := (d1 > d2);     //Сравниваем d1 и d2. Не обязательно так. Зависит от Вашего типа.
  //Сюда можно добавить счетчик сравнений
end;

//Процедура сортировки слияниями
procedure MergeSort(var Arr TArray);
var
  tmp  TArray; //Временный буфер // А где реализация процедуры? Этот код работать не будет, допишите, пожалуйста
  //Слияние
  procedure merge(L, Spl, R  Integer);
  var
    i, j, k  Integer;
  begin
    i := L;
    j := Spl + 1;
    k := ;
    //Выбираем меньший из первых и добавляем в tmp
    while (i <= Spl) and (j <=R) do
    begin
      if IsBigger(Arri, Arrj]) then
      begin
        tmpk := Arrj;
        Inc(j);
      end
      else
      begin
        tmpk := Arri;
        Inc(i);
      end;
      Inc(k);
    end;
    //Просто дописываем в tmp оставшиеся эл-ты
    if i <= Spl then      //Если первая часть не пуста
      for j := i to Spl do
      begin
        tmpk := Arrj;
        Inc(k);
      end
    else                  //Если вторая часть не пуста
      for i := j to R do
      begin
        tmpk := Arri;
        Inc(k);
      end;
    //Перемещаем из tmp в arr
    Move(tmp, ArrL, k*SizeOf(TItem));
  end;

  //Сортировка
  procedure sort(L, R  Integer);
  var
    splitter  Integer;
  begin
    //Массив из 1-го эл-та упорядочен по определению
    if L >= R then Exit;
    splitter := (L + R) div 2;  //Делим массив пополам
    sort(L, splitter);          //Сортируем каждую
    sort(splitter + 1, R);      //часть по отдельности
    merge(L, splitter, R);      //Производим слияние
  end;

  //Основная часть процедуры сортировки
begin
  SetLength(tmp, Length(Arr));
  sort(, Length(Arr) - 1);
  SetLength(tmp, );
end;

end.

Реализация первого этапа

Рекурсивное разбиение массива показано ниже.

Что происходит в этом коде:

1. Функция mergeSort получает исходный массив и левую и правую границы участка, который необходимо отсортировать (индексы start и ).
2. Если длина этого участка больше единицы (), то он разбивается на две части (по индексу ), и каждая из них рекурсивно сортируется.
3. В рекурсивный вызов функции для левой стороны передается начальный индекс участка и индекс . Для правой, соответственно, началом будет , а концом — последний индекс исходного участка.
4. Функция получает две упорядоченных последовательности ( и ) и сливает их с сохранением порядка сортировки.

Механика работы функции merge рассмотрена выше.

Типы сортировок

Сортировка – это процесс перестановки объектов конечного множества в определенном порядке, предназначенный для облегчения последующего поиска элементов в уже отсортированном множестве. Для сортировки можно использовать огромное множество алгоритмов, поэтому часто требуется выполнить сравнительный анализ нескольких алгоритмов, чтобы определить оптимальный выбор для конкретной задачи.

Методы сортировки обычно разделяются на две категории: сортировка массивов и сортировка файлов, также называемые внутренней и внешней сортировкой, так как массивы располагаются во внутренней памяти, а файлы во внешней. Важнейшее требование к алгоритмам для сортировки массивов и связных списков — экономное расходование памяти, поэтому использование дополнительных массивов для сортировки считается дурным тоном.

Основным критерием для классификации алгоритмов сортировки является их быстродействие. При сортировке выполняются два типа операций — сравнение ключей и перестановка элементов (в случае со связными списками — переназначение указателей). Если в массиве n элементов, то алгоритм считается хорошим, если число перестановок равно произведению числа элементов массива n на логарифм этого числа log(n). Например, стандартная пузырьковая сортировка требует числа перестановок, равного квадрату от n.

Методы сортировки можно разбить на три основных класса:

• сортировка включениями;
• сортировка выбором;
• сортировка обменом.

Принцип, лежащий в основе первого класса, заключается в том, что массив разбивается на две половины — итоговую и входную. Берется элемент из входной половины и вставляется в итоговую в порядке сортировки. Число перестановок элементов в общем случае равно квадрату от n.

В случае сортировки выбором алгоритм таков: берется минимальный элемент массива и ставится в начало массива, и т.д. Число перестановок элементов в общем случае меньше, чем в первом случае, и будет равно произведению числа элементов массива на логарифм от этого числа. Быстрая сортировка относится ко второму классу.

Слияние отсортированных участков

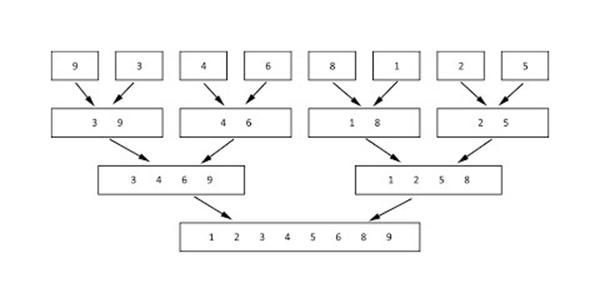
Для понимания алгоритма начнем его разбор с конца — с механизма слияния отсортированных блоков.

Представим, что у нас есть два любым способом отсортированных массива чисел, которые необходимо объединить друг с другом так, чтобы сортировка не нарушилась. Для простоты будем упорядочивать числа по возрастанию.

Элементарный пример: оба массива состоят из одного элемента каждый.

Чтобы слить их, нужно взять нулевой элемент первого массива (не забудьте, что нумерация начинается с нуля) и нулевой элемент второго массива. Это, соответственно, 31 и 18. По условию сортировки число 18 должно идти первым, так как оно меньше. Просто расставляем числа в правильном порядке:

Обратимся к примеру посложнее, в котором каждый массив состоит из нескольких элементов:

Алгоритм слияния будет заключаться в последовательном сравнивании меньших элементов и размещении их в результирующем массиве в правильном порядке. Для отслеживания текущих индексов введем две переменные — index1 и index2. Изначально приравняем их к нулю, так как массивы отсортированы, и самые меньшие элементы стоят в начале.

Распишем по шагам весь процесс слияния:

1. Берем из массива arr1 элемент с индексом index1, а из массива arr2 — с индексом index2.
2. Сравниваем, отбираем наименьший из них и помещаем в результирующий массив.
3. Увеличиваем текущий индекс меньшего элемента на 1.
4. Продолжаем с первого шага.

На первом витке ситуация будет выглядеть так:

На втором витке:

На третьем:

И так далее, пока в итоге не получится полностью отсортированный результирующий массив: {2, 5, 6, 17, 21, 19, 30, 45}.

Определенные сложности могут возникнуть, если сливаются массивы с разными длинами. Что делать, если один из текущих индексов достиг последнего элемента, а во втором массиве еще остаются члены?

Переменная index1 достигла значения 2, однако массив arr1 не имеет элемента с таким индексом. Здесь все просто: достаточно перенести оставшиеся элементы второго массива в результирующий, сохранив их порядок.

Эта ситуация указывает нам на необходимость сопоставлять текущий индекс проверки с длиной сливаемого массива.

Схема слияния упорядоченных последовательностей (A и B) разной длины:

• Если длина обеих последовательностей больше 0, сравнить A и B и переместить меньший из них в буфер.
• Если длина одной из последовательностей равна 0, взять оставшиеся элементы второй последовательности и, не меняя их порядок, перенести в конец буфера.

Паскаль (сортировка текстовых файлов)

Сортировка простым слиянием

Procedure MergeSort(name: string; var f: text);
          Var a1,a2,s,i,j,kol,tmp: integer;
              f1,f2: text;
              b: boolean;
          Begin
             kol:=0;
 
             Assign(f,name);
             Reset(f);
             While not EOF(f) do
               begin
                 read(f,a1);
                 inc(kol);
               End;
             Close(f);
 
             Assign(f1,'{имя 1-го вспомогательного файла}');
             Assign(f2,'{имя 2-го вспомогательного файла}');
 
             s:=1;
             While (s<kol) do
               begin
 
                 Reset(f); Rewrite(f1); Rewrite(f2);
                 For i:=1 to kol div 2 do
                   begin
                     Read(f,a1);
                     Write(f1,a1,' ');
                   End;
                 If (kol div 2) mod s<>0 then
                   begin
                     tmp:=kol div 2;
                     While tmp mod s<>0 do
                       begin
                         Read(f,a1);
                         Write(f1,a1,' ');
                         inc(tmp);
                       End;
                   End;
                 While not EOF(f) do
                   begin
                     Read(f,a2);
                     Write(f2,a2,' ');
                   End;
                 Close(f); Close(f1); Close(f2);
 
 
                 Rewrite(f); Reset(f1); Reset(f2);
                 Read(f1,a1);
                 Read(f2,a2);
                 While (not EOF(f1)) and (not EOF(f2)) do
                   begin
                     i:=0; j:=0;
                     b:=true;
                     While (b) and (not EOF(f1)) and (not EOF(f2)) do
                       begin
                         If (a1<a2) then
                           begin
                             Write(f,a1,' ');
                             Read(f1,a1);
                             inc(i);
                           End
                         else
                           begin
                             Write(f,a2,' ');
                             Read(f2,a2);
                             inc(j);
                           End;
                         If (i=s) or (j=s) then b:=false;
                       End;
                     If not b then
                       begin
                         While (i<s) and (not EOF(f1)) do
                           begin
                             Write(f,a1,' ');
                             Read(f1,a1);
                             inc(i);
                           End;
                         While (j<s) and (not EOF(f2)) do
                           begin
                             Write(f,a2,' ');
                             Read(f2,a2);
                             inc(j);
                           End;
                       End;
                   End;
                 While not EOF(f1) do
                   begin
                     tmp:=a1;
                     Read(f1,a1);
                     If not EOF(f1) then
                       Write(f,tmp,' ')
                     else
                       Write(f,tmp);
                   End;
                 While not EOF(f2) do
                   begin
                     tmp:=a2;
                     Read(f2,a2);
                     If not EOF(f2) then
                       Write(f,tmp,' ')
                     else
                       Write(f,tmp);
                   End;
                 Close(f); Close(f1); Close(f2);
 
                 s:=s*2;
               End;
             Erase(f1);
             Erase(f2);
          End;

Сортировка естественным слиянием

Procedure MergeSort(name: string; var f: text);
          Var s1,s2,a1,a2,where,tmp: integer;
              f1,f2: text;
          Begin
             s1:=5; s2:=5; {Можно задать любые числа, которые запустят цикл while}
             Assign(f,name);
             Assign(f1,'{имя 1-го вспомогательного файла}');
             Assign(f2,'{имя 2-го вспомогательного файла}');
             While (s1>1) and (s2>=1) do
               begin
                 where:=1;
                 s1:=0; s2:=0;
                 Reset(f); Rewrite(f1); Rewrite(f2);
                 Read(f,a1);
                 Write(f1,a1,' ');
                 While not EOF(f) do
                   begin
                     read(f,a2);
                     If (a2<a1) then
                       begin
                         Case where of
                            1: begin
                                 where:=2;
                                 inc(s1);
                               End;
                            2: begin
                                 where:=1;
                                 inc(s2);
                               End;
                         End;
                       End;
                     Case where of
                        1: write(f1,a2,' ');
                        2: write(f2,a2,' ');
                     End;
                     a1:=a2;
                   End;
                 If where=2 then
                   inc(s2)
                 else
                   inc(s1);
                 Close(f); Close(f1); Close(f2);
 
 
                 Rewrite(f); Reset(f1); Reset(f2);
                 Read(f1,a1);
                 Read(f2,a2);
                 While (not EOF(f1)) and (not EOF(f2)) do
                   begin
                     If (a1<=a2) then
                       begin
                         Write(f,a1,' ');
                         Read(f1,a1);
                       End
                     else
                       begin
                         Write(f,a2,' ');
                         Read(f2,a2);
                       End;
                   End;
                 While not EOF(f1) do
                   begin
                     tmp:=a1;
                     Read(f1,a1);
                     If not EOF(f1) then
                        Write(f,tmp,' ')
                     else
                        Write(f,tmp);
                   End;
                 While not EOF(f2) do
                   begin
                     tmp:=a2;
                     Read(f2,a2);
                     If not EOF(f2) then
                        Write(f,tmp,' ')
                     else
                        Write(f,tmp);
                   End;
                 Close(f); Close(f1); Close(f2);
               End;
             Erase(f1);
             Erase(f2);
          End;

Слияние за линейное время

O(N)

• Выбираем число S≈sqrt(N)
• Делим массив на K кусков длины S. Остаток, не попавший ни в один из кусков, пока не трогаем
• Кусок, в который попала граница между упорядоченными фрагментами, меняем с последним куском. Это будет наш буфер обмена
• Сортируем K-1 оставшийся кусок по возрастанию первых элементов. Здесь нам нужно использовать алгоритм, линейный по числу обменов. Подходит сортировка выбором минимального элемента.
• Замечаем две важные вещи. Во-первых, если у нас есть два поряд идущих отсортированных фрагмента длиной A и B и буфер обмена, длина которого не меньше min(A,B), то мы можем слить эти фрагменты, затратив не более A+B сравнений и A+B+min(A,B) обменов. Порядок элементов в буфере обмена при этом может измениться. Во-вторых, при сортировке полученного на предыдущем шаге массива из (K-1)*S элементов, каждый элемент может сдвинуться не более, чем на S позиций влево, т.е. никогда не окажется левее предыдущего «куска».
• Пользуясь буфером обмена, последовательно сливаем пары соседних кусков – и , потом и , и т.д. Из предыдущего пункта следует, что в результате мы получим отсортированный массив из M=S*(K-1) элементов
• Сортируем последние R=N-M элементов исходного массива (буфер обмена+остаток) любым алгоритмом. Они рекомендуют какой-нибудь квадратичный алгоритм (для чистоты идеи, чтобы избежать рекурсии), но с практической точки зрения, рекурсивный вызов сортировки не хуже.
• Сливаем отсортированные фрагменты массива и , используя фрагмент как буфер обмена
• Ищем на стыке предыдущего и следующего пунктов ошибку в алгоритме. Если не найдете – она объясняется в конце статьи
• Сортируем буфер обмена: в нем были и остались R младших элементов массива, и после сортировки они окажутся на месте

5*N6*Nlog(N)

Сортировка с однопоточным слиянием[править]

Внесем в алгоритм сортировки слиянием следующую модификацию: будем сортировать левую и правую части массива параллельно.

   function mergeSortMT(array, left, right):
       mid = (left + right) / 2
   
       spawn mergeSortMT(array, left, mid)
       mergeSortMT(array, mid + 1, right)
       sync
   
       merge(array, left, mid, right)

В данном алгоритме оператор запускает новый поток, а оператор ожидает завершения этого потока. Функция аналогична одноименной функции из раздела .
Несмотря на наличие двух рекурсивных вызовов, при оценке будем считать, что совершается один вызов, т.к. оба вызова выполняются параллельно с одинаковой асимптотикой. Оценим время работы данного алгоритма: . Данная асимптотика достигается при возможности запускать неограниченное количество потоков независимо друг от друга.

Implementing Merge Sort Algorithm

Below we have a C program implementing merge sort algorithm.

Given array:
32 45 67 2 7
Sorted array:
2 7 32 45 67

Complexity Analysis of Merge Sort

Merge Sort is quite fast, and has a time complexity of . It is also a stable sort, which means the «equal» elements are ordered in the same order in the sorted list.

In this section we will understand why the running time for merge sort is .

As we have already learned in Binary Search that whenever we divide a number into half in every step, it can be represented using a logarithmic function, which is and the number of steps can be represented by (at most)

Also, we perform a single step operation to find out the middle of any subarray, i.e. .

And to merge the subarrays, made by dividing the original array of elements, a running time of will be required.

Hence the total time for function will become , which gives us a time complexity of .

Worst Case Time Complexity : O(n*log n)

Best Case Time Complexity : O(n*log n)

Average Time Complexity : O(n*log n)

Space Complexity: O(n)

• Time complexity of Merge Sort is in all the 3 cases (worst, average and best) as merge sort always divides the array in two halves and takes linear time to merge two halves.
• It requires equal amount of additional space as the unsorted array. Hence its not at all recommended for searching large unsorted arrays.
• It is the best Sorting technique used for sorting Linked Lists.

• ← Prev
• Next →

Оценка работы метода

Временная сложность сортировки слиянием определяется высотой дерева разбиений алгоритма и равна количеству элементов в массиве (n), умноженному на его логарифм (log n). Такая оценка называется логарифмической.

Это одновременно и достоинство, и недостаток метода. Время его работы не меняется даже в худшем случае, когда исходный массив отсортирован в обратном порядке. Однако при обработке полностью отсортированных данных алгоритм не обеспечивает выигрыша во времени.

Важно отметить и затраты памяти при работе метода сортировки слиянием. Они равны размеру исходной коллекции

В этой дополнительно выделенной области из кусочков собирается отсортированный массив.

Java

Итерационный алгоритм:

public static void selectionSort (int[] numbers){
    int min, temp;
 
    for (int index = 0; index < numbers.length-1; index++){
        min = index;
        for (int scan = index+1; scan < numbers.length; scan++)
            if (numbers < numbers)
                min = scan;
 
        // Swap the values
        temp = numbers;
        numbers = numbers;
        numbers = temp;
    }
}

Рекурсивный алгоритм:

public static int findMin(int[] array, int index){
    int min = index - 1;
    if(index < array.length - 1) min = findMin(array, index + 1);
    if(array < array) min = index;
    return min;
}
 
public static void selectionSort(int[] array){
    selectionSort(array, 0);
}
 
public static void selectionSort(int[] array, int left){
    if (left < array.length - 1) {
        swap(array, left, findMin(array, left));
        selectionSort(array, left+1);
    }
}
 
public static void swap(int[] array, int index1, int index2) {
    int temp = array;
    array = array;
    array = temp;
}

Паскаль (сортировка текстовых файлов)[править]

Сортировка простым слияниемправить

Procedure MergeSort(name string; var f text); 
          Var a1,a2,s,i,j,kol,tmp integer;
              f1,f2 text;
              b boolean;
          Begin
             kol:=;

             Assign(f,name);
             Reset(f);
             While not EOF(f) do
               begin
                 read(f,a1);
                 inc(kol);
               End;
             Close(f);

             Assign(f1,'{имя 1-го вспомогательного файла}');
             Assign(f2,'{имя 2-го вспомогательного файла}');

             s:=1;
             While (s<kol) do
               begin

                 Reset(f); Rewrite(f1); Rewrite(f2);
                 For i:=1 to kol div 2 do
                   begin
                     Read(f,a1);
                     Write(f1,a1,' ');
                   End;
                 If (kol div 2) mod s<> then
                   begin
                     tmp:=kol div 2;
                     While tmp mod s<> do
                       begin
                         Read(f,a1);
                         Write(f1,a1,' ');
                         inc(tmp);
                       End;
                   End;
                 While not EOF(f) do
                   begin
                     Read(f,a2);
                     Write(f2,a2,' ');
                   End;
                 Close(f); Close(f1); Close(f2);


                 Rewrite(f); Reset(f1); Reset(f2);
                 Read(f1,a1);
                 Read(f2,a2);
                 While (not EOF(f1)) and (not EOF(f2)) do
                   begin
                     i:=; j:=;
                     b:=true;
                     While (b) and (not EOF(f1)) and (not EOF(f2)) do
                       begin
                         If (a1<a2) then
                           begin
                             Write(f,a1,' ');
                             Read(f1,a1);
                             inc(i);
                           End
                         else
                           begin
                             Write(f,a2,' ');
                             Read(f2,a2);
                             inc(j);
                           End;
                         If (i=s) or (j=s) then b:=false;
                       End;
                     If not b then
                       begin
                         While (i<s) and (not EOF(f1)) do
                           begin
                             Write(f,a1,' ');
                             Read(f1,a1);
                             inc(i);
                           End;
                         While (j<s) and (not EOF(f2)) do
                           begin
                             Write(f,a2,' ');
                             Read(f2,a2);
                             inc(j);
                           End;
                       End;
                   End;
                 While not EOF(f1) do
                   begin
                     tmp:=a1;
                     Read(f1,a1);
                     If not EOF(f1) then
                       Write(f,tmp,' ')
                     else
                       Write(f,tmp);
                   End;
                 While not EOF(f2) do
                   begin
                     tmp:=a2;
                     Read(f2,a2);
                     If not EOF(f2) then
                       Write(f,tmp,' ')
                     else
                       Write(f,tmp);
                   End;
                 Close(f); Close(f1); Close(f2);

                 s:=s*2;
               End;
             Erase(f1);
             Erase(f2);
          End;

Сортировка естественным слияниемправить

Procedure MergeSort(name string; var f text);
          Var s1,s2,a1,a2,where,tmp integer;
              f1,f2 text;
          Begin
             s1:=5; s2:=5; {Можно задать любые числа, которые запустят цикл while}
             Assign(f,name);
             Assign(f1,'{имя 1-го вспомогательного файла}');
             Assign(f2,'{имя 2-го вспомогательного файла}');
             While (s1>1) and (s2>=1) do
               begin
                 where:=1;
                 s1:=; s2:=;
                 Reset(f); Rewrite(f1); Rewrite(f2);
                 Read(f,a1);
                 Write(f1,a1,' ');
                 While not EOF(f) do
                   begin
                     read(f,a2);
                     If (a2<a1) then
                       begin
                         Case where of
                            1 begin
                                 where:=2;
                                 inc(s1);
                               End;
                            2 begin
                                 where:=1;
                                 inc(s2);
                               End;
                         End;
                       End;
                     Case where of
                        1 write(f1,a2,' ');
                        2 write(f2,a2,' ');
                     End;
                     a1:=a2;
                   End;
                 If where=2 then
                   inc(s2)
                 else
                   inc(s1);
                 Close(f); Close(f1); Close(f2);


                 Rewrite(f); Reset(f1); Reset(f2);
                 Read(f1,a1);
                 Read(f2,a2);
                 While (not EOF(f1)) and (not EOF(f2)) do
                   begin
                     If (a1<=a2) then
                       begin
                         Write(f,a1,' ');
                         Read(f1,a1);
                       End
                     else
                       begin
                         Write(f,a2,' ');
                         Read(f2,a2);
                       End;
                   End;
                 While not EOF(f1) do
                   begin
                     tmp:=a1;
                     Read(f1,a1);
                     If not EOF(f1) then
                        Write(f,tmp,' ')
                     else
                        Write(f,tmp);
                   End;
                 While not EOF(f2) do
                   begin
                     tmp:=a2;
                     Read(f2,a2);
                     If not EOF(f2) then
                        Write(f,tmp,' ')
                     else
                        Write(f,tmp);
                   End;
                 Close(f); Close(f1); Close(f2);
               End;
             Erase(f1);
             Erase(f2);
          End;

Принцип работы[править]

Пример работы процедуры слияния.

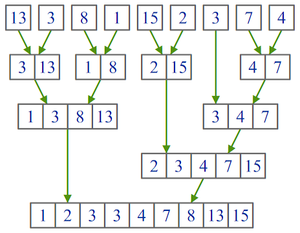
Пример работы рекурсивного алгоритма сортировки слиянием

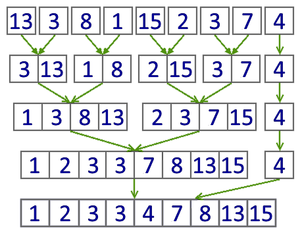
Пример работы итеративного алгоритма сортировки слиянием

Алгоритм использует принцип «разделяй и властвуй»: задача разбивается на подзадачи меньшего размера, которые решаются по отдельности, после чего их решения комбинируются для получения решения исходной задачи. Конкретно процедуру сортировки слиянием можно описать следующим образом:

1. Если в рассматриваемом массиве один элемент, то он уже отсортирован — алгоритм завершает работу.
2. Иначе массив разбивается на две части, которые сортируются рекурсивно.
3. После сортировки двух частей массива к ним применяется процедура слияния, которая по двум отсортированным частям получает исходный отсортированный массив.

Слияние двух массивовправить

У нас есть два массива и (фактически это будут две части одного массива, но для удобства будем писать, что у нас просто два массива). Нам надо получить массив размером . Для этого можно применить процедуру слияния. Эта процедура заключается в том, что мы сравниваем элементы массивов (начиная с начала) и меньший из них записываем в финальный. И затем, в массиве у которого оказался меньший элемент, переходим к следующему элементу и сравниваем теперь его. В конце, если один из массивов закончился, мы просто дописываем в финальный другой массив. После мы наш финальный массив записываем заместо двух исходных и получаем отсортированный участок.

Множество отсортированных списков с операцией является моноидом, где нейтральным элементом будет пустой список.

Ниже приведён псевдокод процедуры слияния, который сливает две части массива — и

function merge(a : int; left, mid, right : int):
    it1 = 0
    it2 = 0
    result : int
  
    while left + it1 < mid and mid + it2 < right
        if a < a
            result = a
            it1 += 1
        else
            result = a
            it2 += 1
  
    while left + it1 < mid
        result = a
        it1 += 1
  
    while mid + it2 < right
        result = a
        it2 += 1
  
    for i = 0 to it1 + it2
        a = result

Рекурсивный алгоритмправить

Функция сортирует подотрезок массива с индексами в полуинтервале .

function mergeSortRecursive(a : int; left, right : int):
    if left + 1 >= right
        return
    mid = (left + right) / 2
    mergeSortRecursive(a, left, mid)
    mergeSortRecursive(a, mid, right)
    merge(a, left, mid, right)

Итеративный алгоритмправить

При итеративном алгоритме используется на меньше памяти, которая раньше тратилась на рекурсивные вызовы.

function mergeSortIterative(a : int):
    for i = 1 to n, i *= 2
        for j = 0 to n - i, j += 2 * i
            merge(a, j, j + i, min(j + 2 * i, n))

Оптимальный порядок слияния

С отдельными слияниями разобрались, но что с сортировкой в целом? Первое, что стоит сделать, это улучшить случай отсортированного массива. Для этого необходимо не просто разрезать массив на подмассивы одинаковой длинны \(2^j\), а выбирать максимально длинные отсортированные части. Кроме того можно выбирать не только подмассивы, отсортированные в нужном нам порядке, но и обратно отсортированные, меняя для них направление итератора. Таким образом можно получить список подмассивов оригинального массива, для каждого подмассива необходима пара чисел: начало и конец. При этом, если начало больше конца, значит подмассив обратно отсортирован.

И тут возникает следующий вопрос: в каком порядке сливать полученные подмассивы? Для того, чтобы более наглядно фиксировать порядок слияния, будем использовать дерево слияния.

graph TD
ABCD
ABCD—AB
AB—A
AB—B
ABCD—CD
CD—C
CD—D
style A fill:LightCoral
style B fill:SpringGreen
style C fill:SkyBlue
style D fill:MediumPurple
style AB fill:Yellow
style CD fill:Cyan
style ABCD fill:White

Рис. 1.

Ниже в узлах дерева будем записывать только размеры подмассивов.

graph TD
ABCD((24))
ABCD—AB((18))
AB—A((2))
AB—B((16))
ABCD—CD((6))
CD—C((3))
CD—D((3))
style A fill:LightCoral
style B fill:SpringGreen
style C fill:SkyBlue
style D fill:MediumPurple
style AB fill:Yellow
style CD fill:Cyan
style ABCD fill:White

Рис. 2.

В данном случае это минимальное по глубине дерево. Такое дерево легко получить при обработке подмассивов в порядке расположения. Однако, это не всегда выигрышный подход, как и в этом примере. Надо помнить, что сложность функции слияния зависит от размеров сливаемых частей. И это дерево не является оптимальным, потому что самый большой подмассив, состоящий из \(16\) элементов мы сливали дважды. Более оптимальным в данном случае будет следующее дерево слияния:

graph TD
ABCD((24))
ABCD—ACD((8))
ACD—AC((5))
AC—A((2))
AC—C((3))
ACD—D((3))
ABCD—B((16))
style A fill:LightCoral
style B fill:SpringGreen
style C fill:SkyBlue
style D fill:MediumPurple
style AC fill:#b666d2
style ACD fill:#df00ff
style ABCD fill:White

Рис. 3.

Лучшим деревом слияния будет то, где каждый раз сливаются массивы минимальной длинны из оставшихся. Для его построения воспользуемся следующей леммой:

Лемма

Пусть \(X = ( x_i \colon i < k )\) конечная последовательность натуральных чисел. Будем строить последовательность \(Y\) следующим образом:

• выберем и вычеркнем из \(X \cup Y\) два минимальных числа \(a\) и \(b\);
• добавим в \(Y\) число \(a + b\);
• повторяем до тех пор, пока \(|X \cup Y| \geqslant 2\).

Тогда на каждом шаге \(a + b \geqslant \max Y\).

Доказательство достаточно тривиально и оставляется на откуп читателю ().

Куда труднее эту лемму применить. Для оптимального слияния необходимо правильно расположить начальные подмассивы друг относительно друга так, чтобы всегда сливались соседние. Расположить подмассивы просто в порядке возрастания их длин неверное решение, например, если у нас есть подмассивы длин \((1, 2, 2, 2, 3)\), то последний подмассив надо перенести в середину:

graph TD
ABCDE((10))
ABCDE—ABE((6))
ABE—AB((3))
AB—A((1))
AB—B((2))
ABCDE—CD((4))
CD—C((2))
CD—D((2))
ABE—E((3))
style E fill:pink

Рис. 4.

Релизация подобной перестановки оставляется читателю.

Divide and Conquer

If we can break a single big problem into smaller sub-problems, solve the smaller sub-problems and combine their solutions to find the solution for the original big problem, it becomes easier to solve the whole problem.

Let’s take an example, Divide and Rule.

When Britishers came to India, they saw a country with different religions living in harmony, hard working but naive citizens, unity in diversity, and found it difficult to establish their empire. So, they adopted the policy of Divide and Rule. Where the population of India was collectively a one big problem for them, they divided the problem into smaller problems, by instigating rivalries between local kings, making them stand against each other, and this worked very well for them.

Well that was history, and a socio-political policy (Divide and Rule), but the idea here is, if we can somehow divide a problem into smaller sub-problems, it becomes easier to eventually solve the whole problem.

In Merge Sort, the given unsorted array with elements, is divided into subarrays, each having one element, because a single element is always sorted in itself. Then, it repeatedly merges these subarrays, to produce new sorted subarrays, and in the end, one complete sorted array is produced.

The concept of Divide and Conquer involves three steps:

1. Divide the problem into multiple small problems.
2. Conquer the subproblems by solving them. The idea is to break down the problem into atomic subproblems, where they are actually solved.
3. Combine the solutions of the subproblems to find the solution of the actual problem.

C++[править]

/**
* @brief         Сортировка элементов от left до right массива buf
* @param[in/out] buf - сортируемый массив
* @param     left - левая граница. При первой итерации left = 0
* @param     right - правая граница. При первой итерации right = buf.size() - 1
*
* В результате сортируются все элементы массива buf от left до right включительно.
*/
template<typename Type>
void MergeSort(vector<Type>& buf, size_t left, size_t right)
{
    //! Условие выхода из рекурсии
    if(left >= right) return;

    size_t middle = left + (right - left)  2;

    //! Рекурсивная сортировка полученных массивов
    MergeSort(buf, left, middle);
    MergeSort(buf, middle + 1, right);
    merge(buf, left, right, middle);
}

/**
 * @brief Слияние элементов.
 * @param[in/out] buf - массив
 * @param     left - левая граница. При певой итерации left = 0
 * @param     right - правая граница. При первой итерации right = buf.size() - 1
 * @param     middle - граница подмассивов.
 *
 * Массив buf содержит два отсортированных подмассива:
 * -  - первый отсортированный подмассив.
 * -  - второй отсортированный подмассив.
 * В результате получаем отсортированный массив, полученный из двух подмассивов,
 * который сохраняется в buf.
 */
template<typename Type>
static void merge(vector<Type>& buf, size_t left, size_t right, size_t middle)
{
    if (left >= right || middle < left || middle > right) return;
    if (right == left + 1 && bufleft > bufright]) {
        swap(bufleft], bufright]);
        return;
    }

    vector<Type> tmp(&bufleft], &bufright + 1));

    for (size_t i = left, j = , k = middle - left + 1; i <= right; ++i) {
        if (j > middle - left) {      
            bufi = tmpk++];
        } else if(k > right - left) {
            bufi = tmpj++];
        } else {
            bufi = (tmpj < tmpk]) ? tmpj++  tmpk++];
        }
    }
}

Существует также итеративный алгоритм сортировки, избавленный от рекурсивных вызовов. Такой алгоритм называют «Восходящей сортировкой слиянием».

/*
* Слияние двух упорядоченных массивов
* m1 - Первый массив
* m2 - Второй массив
* len_1 - Длина первого массива
* len_2 - Длина второго массива
* Возвращает объединённый массив
*/
template <class T>
T* merge(T *m1, T* m2, int len_1, int len_2)
{
    T* ret = new Tlen_1+len_2];
    int n = ;
    // Сливаем массивы, пока один не закончится
    while (len_1 && len_2) {
        if (*m1 < *m2) {
            retn = *m1;
            m1++;
            --len_1;
        } else {
            retn = *m2;
            ++m2;
            --len_2;
        }
        ++n;
    }
    // Если закончился первый массив
    if (len_1 == ) {
        for (int i = ; i < len_2; ++i) {
            retn++ = *m2++;
        }
    } else { // Если закончился второй массив
        for (int i = ; i < len_1; ++i) {
            retn++ = *m1++;
        }
    }
    return ret;
}

// Функция восходящего слияния
template <class T>
void mergeSort(T * mas, int len)
{
    int n = 1, k, ost;
    T * mas1;
    while (n < len) {
        k = ;
        while (k < len) {
            if (k + n >= len) break;
            ost = (k + n * 2 > len) ? (len - (k + n))  n;
            mas1 = merge(mas + k, mas + k + n, n, ost);
            for (int i = ; i < n + ost; ++i)
                mask+i = mas1i];//тут нужно что-то поменять, потому что это лишнее копирование, и оно увеличивает время работы алгоритма в два раза
            delete [] mas1;
            k += n * 2;
        }
        n *= 2;
    }
}

Пример:
char a[] = «ASORTINGEXAMPLE»;
mergeSort(a, 16);
Альтернативная версия алгоритма Сортировки Слиянием.

               template <typename Item>
void Merge(Item Mas[], int left, int right, int medium)
{
    int j = left;
    int k = medium + 1;
    int count = right - left + 1;

    if (count <= 1) return;

    Item *TmpMas = new Itemcount];

    for (int i = ; i < count; ++i) {
        if (j <= medium && k <= right) {
            if (Masj < Mask])
                TmpMasi = Masj++];
            else
                TmpMasi = Mask++];
        } else {
            if (j <= medium)
                TmpMasi = Masj++];
            else
                TmpMasi = Mask++];
        }
    }

    j = ;
    for (int i = left; i <= right; ++i) {
        Masi = TmpMasj++];
    }
    delete[] TmpMas;
}

template <typename Item>
void MergeSort(Item a[], int left, int right)
{
    int middle;

    // Условие выхода из рекурсии
    if(left >= right) return;

    middle = left + (right - left)  2;

    // Рекурсивная сортировка полученных массивов
    MergeSort(a, left, middle);
    MergeSort(a, middle + 1, right);
    Merge(a, left, right, middle);
}

Метод нисходящего слияния

Исходная последовательность рекурсивно разбивается на половины, пока не получим подпоследовательности по 1 элементу. Из полученных подпоследовательностей формируем упорядоченные пары методом слияния, затем — упорядоченные четверки и т.д.
Рассмотрим последовательность
Разбиваем последовательность на 2 половины (рекурсивно, пока не получим пары).
Каждую подпоследовательность упорядочиваем методом слияния и получаем готовую последовательность.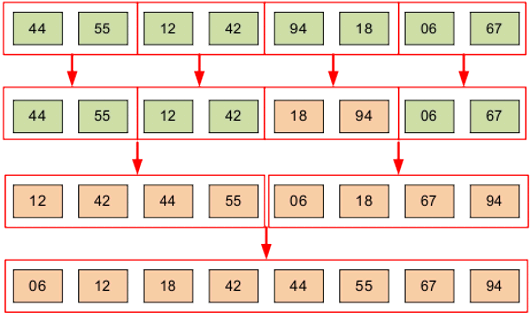Реализация метода нисходящего слияния на Си

1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950

#include <stdio.h>#include <stdlib.h>#define SIZE 16// Функция сортировки нисходящим слияниемvoid mergeSort(int *a, int l, int r){  if (l == r) return; // границы сомкнулись  int mid = (l + r) / 2; // определяем середину последовательности  // и рекурсивно вызываем функцию сортировки для каждой половины  mergeSort(a, l, mid);  mergeSort(a, mid + 1, r);  int i = l;  // начало первого пути  int j = mid + 1; // начало второго пути  int *tmp = (int*)malloc(r * sizeof(int)); // дополнительный массив  for (int step = 0; step < r — l + 1; step++) // для всех элементов дополнительного массива  {    // записываем в формируемую последовательность меньший из элементов двух путей    // или остаток первого пути если j > r    if ((j > r) || ((i <= mid) && (a < a)))     {      tmp = a;      i++;    }    else     {      tmp = a;      j++;    }  }  // переписываем сформированную последовательность в исходный массив  for (int step = 0; step < r — l + 1; step++)    a = tmp;}int main() {  int a;  // Заполняем элементы массива  for (int i = 0; i<SIZE; i++)   {    a = (rand() % 100);    printf(» %d «, a);  }  mergeSort(a, 0, SIZE — 1); // вызываем функцию сортировки  printf(«\n»);  // Выводим отсортированный массив  for (int i = 0; i<SIZE; i++)    printf(» %d «, a);  getchar();  return 0;}