Знак ровно

Математические знаки

Скорее всего, к первому классу ребенок уже отличает на слух и визуально, что горстка из десяти ягод больше трех штук. Чтобы внедрить в жизнь новые обозначения, посмотрим на знаки «больше», «меньше», «равно» в картинках.

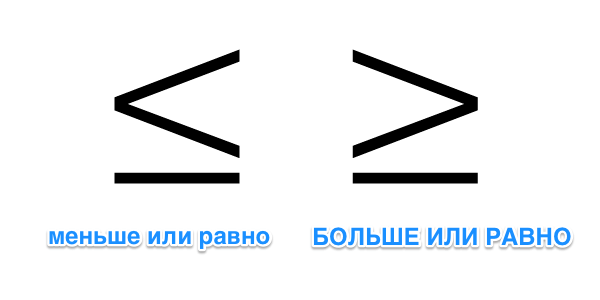
Символ больше (>) — это когда острый нос галочки смотрит направо. Его нужно использовать, когда первое число больше второго:

Символ меньше (<) — это когда острый нос галочки смотрит налево. Его нужно использовать, когда первое число меньше второго:

Символ равенства (=) — это когда два коротких отрезка записаны горизонтально и параллельны друг другу. Используем его при сравнении двух одинаковых чисел:

Чтобы ребенку было легче запомнить схожие между собой знаки, можно применить игровой метод. Для этого нужно сравнить числа и определить в каком порядке они стоят. Далее ставим одну точку у наименьшего числа и две — рядом с наибольшим. Соединяем точки и получаем нужный знак. Вот так просто: 

Неправильное использование

Знак равенства иногда используется неправильно в математическом аргументе, чтобы соединить шаги математики нестандартным способом, а не для демонстрации равенства (особенно ранними учениками математики).

Например, если кто-то находил сумму, шаг за шагом, чисел 1, 2, 3, 4 и 5, можно было бы неправильно написать:

1 + 2 = 3 + 3 = 6 + 4 = 10 + 5 = 15.

Структурно это сокращение для:

( + 4 = 10) + 5 = 15,

но запись неверна, потому что каждая часть равенства имеет разное значение. Если интерпретировать строго так, как говорится, это будет означать, что:

3 = 6 = 10 = 15 = 15.

Правильная версия аргумента будет:

1 + 2 = 3, 3 + 3 = 6, 6 + 4 = 10, 10 + 5 = 15.

Эта трудность возникает из-за различного использования знака в образовании. В начале, арифметика ориентированных классов, то знак равенства может быть оперативно ; как кнопка равенства на электронном калькуляторе, он требует результата вычисления. Начиная с курсов алгебры, этот знак приобретает относительный смысл равенства между двумя вычислениями. Путаница между двумя видами использования знака иногда сохраняется на университетском уровне.

Синонимы: краткий справочник

найдено словарных статей: 6 аутентическийаутентичныйидентичныйодинаковыйравновеликийравнозначныйравносильныйравноценныйравныйровныйтождественныйэквивалентныйапатичныйбездеятельныйбезразличныйбезучастныйбезынициативныйглухойиндифферентныйинертныйледянойравнодушныйаутентическийаутентичныйидентичныйодинаковыйравновеликийравнозначныйравносильныйравноценныйравныйровныйтождественныйэквивалентныймерныйплавныйравномерныйразмеренныйритмическийритмичныйаутентическийаутентичныйидентичныйодинаковыйравновеликийравнозначныйравносильныйравноценныйравныйровныйтождественныйэквивалентныйаутентическийаутентичныйидентичныйодинаковыйравновеликийравнозначныйравносильныйравноценныйравныйровныйтождественныйэквивалентный

Ход урока

2. Основная часть:

Учитель: А совершим мы с вами сегодня полёт в неизведанное космическое пространство. Сегодня мы будем не учениками, а исследователями космического пространства. А чтобы полёт прошёл удачно давайте вспомним, чем мы занимаемся на уроках математики?

Ученики: Решаем, считаем, пишем, думаем…

Учитель: А как вы думаете, что мы будем делать сегодня?

Ученики: Считать, решать, отвечать, думать, чертить…

Учитель: Чтобы полёт прошёл удачно, необходимо быть:

• Внимательными
• Точно и правильно выполнять задания
• Не допускать ошибок, иначе ракета может потерпеть аварию.

Учитель: Итак, повышенное внимание! До старта ракеты осталось 10 секунд, давайте немного посчитаем. (Ученики ведут счёт)

• Счёт цепочкой до 10.
• Начинает учитель, дети продолжают.
• Отсчёт в обратном направлении.
• Отсчитываем секунды 10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0 пуск. Мы в полёте!

Учитель: Ребята, посмотрите на доску, она сегодня превратилась в «звёздное небо». Но какие необычные звёзды! Что они нам напоминают?

Ученики: геометрические фигуры.

Учитель: Что это за фигуры, назовите.

Ученики: отрезок, прямая, точки, ломаная, кривая.

Учитель: Пока мы смотрели на небо глазки устали, давайте сделаем для них зарядку.

Учитель: Ребята, посмотрите, наш пульт управления находится в аварийном состоянии. Запали кнопки, необходимо исправить пульт.

• Какое число идёт при счёте за числом 3, 6, 9?
• Какое число стоит перед числом 2, 5, 8, 10?
• Назовите соседей числа 2, 7?

Но на пульте кроме цифр есть ещё различные знаки, они тоже стёрлись, давайте их восстановим (дети по очереди отвечают, остальные хлопают в ладоши, если верно)

2 3=5		4 =2
5 1=4		1+ =4
3+ =5		5- =4

Молодцы! Пульт исправен.

Учитель: Пока наша ракета поднимается ввысь, поиграем в игру «Сложи фигуру».

Нужно из палочек сложить фигуру, состоящую из четырёх квадратов.

Посчитай сколько здесь квадратов? (фигура состоит из 4 квадратов)

Переложи 2 палочки так, чтобы получилось 5 одинаковых квадратов.

Наша ракета всё дальше и дальше удаляется от Земли, как приятно вспомнить всё, что связано с землёй. Представьте, что мы на большой лесной полянке.

Физминутка: (негромко звучит весёлая музыка)

Учитель: А сейчас приготовьте свои квадраты. Положите в верхний ряд 2 зелёных квадрата, а в нижний 3 синих.

Каких квадратов меньше?

Какое число меньше 2 или 3?

В математике есть специальная запись. Это записывают так: 2<3

< – знак меньше

Каких квадратов больше? (синих)

Какое число больше? (3)

Кто догадался, как это записать? 3>2

> – знак больше

Знак ставится так, чтобы к большему числу «клювик» был открыт.

Давайте отдохнём и посмотрим телевизор, что у нас сегодня показывают (работа с учебником, выполнение задания).

• Сколько было птичек на первой картинке
• Сколько прилетело
• Сколько стало
• Их стало больше или меньше
• Как это записали, прочитайте
• Сколько ягод на кисточке
• Что произошло с ягодами
• Как это записать
• Какое число больше, меньше?

Учитель: Наша ракета стремительно несётся ввысь. Экипаж работает слаженно, чётко. Сейчас серьёзная работа, мы выходим в открытый космос. О, я вижу планету, от неё отделяется какой-то неожиданный летающий объект. Что это? Инопланетяне хотят уничтожить нашу ракету. Приготовьтесь к математическому сражению. А оружием будет ум и смелость. Я показываю пример, вы с помощью веера цифр ответ.

У кого можно попросить помощи, если очень трудно? (соседа по парте)

2+2		1+2		4-2
3+2		3-1		5-3

– Мы победили, корабль удаляется. Заполним ботржурналы. Проверьте рабочее место, сядьте поудобнее, чтобы бортжурналы лежали правильно, записи были чёткими и аккуратными. Работаем на странице 11. (работа в тетрадях на печатной основе для 1 класса)

– Перед вами знаки. Как называется первый знак? (больше)

Как называется второй знак? (меньше)

Напишите знак по точкам, допишите до конца строки.

Учитель: Перед стартом ракеты я предлагаю вам поработать в паре. У вас на столах карточки, нужно вставить недостающие знаки «больше» или «меньше».

Карточка.

2*3		5*7		8*5
5*3		10*7		6*2
3*9		7*1		6*9

3. Рефлексия:

Благодаря дружной работе наша ракета совершила мягкую посадку. Во время полёта мы провели большую работу.

– Скажите, что вы для себя узнали нового?

– Чем мы сегодня занимались?

– Что вам помогло хорошо работать на уроке?

У вас на столах лежат мордочки, нарисуйте на них выражения лица весёлое или грустное, кому на уроке было хорошо поднимите весёлую мордочку. А у кого что-то не получилось и было грустно? (таких может не быть)

Полёт завершён, всем спасибо!

Использование в математике и компьютерном программировании

В математике знак равенства может использоваться как простое изложение факта в конкретном случае ( ) или для создания определений ( ), условных утверждений ( ) или для выражения универсальной эквивалентности ( ).

Первым важным языком компьютерного программирования, в котором использовался знак равенства, была оригинальная версия Fortran , FORTRAN I, разработанная в 1954 году и реализованная в 1957 году. В Фортране = служит оператором присваивания : устанавливает значение в 2. Это несколько напоминает оператор использование = в математическом определении, но с другой семантикой: выражение, следующее за = , вычисляется первым и может относиться к предыдущему значению . Например, присвоение увеличивает значение на 2.

Пионером в использовании конкурирующего языка программирования стала оригинальная версия ALGOL , которая была разработана в 1958 году и реализована в 1960 году. Алгол включал в себя оператор отношения, который проверял равенство, позволяя конструкции вроде с тем же значением =, что и условное использование в математика. Знак равенства был зарезервирован для этого использования.

Оба использования оставались распространенными в разных языках программирования до начала 21 века. Как и в Fortran, = используется для присваивания в таких языках, как C , Perl , Python , awk и их потомках. Но = используется для равенства, а не присваивания в семействе Pascal , Ada , Eiffel , APL и других языках.

В некоторых языках, таких как BASIC и PL / I , знак равенства используется для обозначения как присвоения, так и равенства, различаемых контекстом. Однако в большинстве языков, где = имеет одно из этих значений, для другого значения используется другой символ или, чаще, последовательность символов. Следуя ALGOL, большинство языков, которые используют = для равенства, используют : = для присваивания, хотя APL с его специальным набором символов использует стрелку, указывающую влево.

В Фортране не было оператора равенства (можно было сравнить выражение с нулем только с помощью арифметического оператора IF ) до выпуска FORTRAN IV в 1962 году, с тех пор, когда он использовал четыре символа для проверки равенства. Язык B представил использование == с этим значением, которое было скопировано его потомком C и большинством более поздних языков, где = означает присваивание.

Знак равенства также используется при определении пар атрибут – значение , в котором атрибуту присваивается значение .

Использование нескольких знаков равенства

В PHP , то знак тройной равно , обозначает значение и тип равенства, а это означает , что не только эти два выражения вычисляются одинаковые значения, но они также одного и того же типа данных. Например, выражение истинно, но не так, потому что число 0 является целым числом, а ложь — логическим значением.

JavaScript имеет ту же семантику , которая называется «равенство без приведения типов». Однако в JavaScript поведение не может быть описано какими-либо простыми последовательными правилами. Выражение истинно, но ложно, даже если обе стороны действия одинаковы в логическом контексте. По этой причине иногда рекомендуется избегать оператора в JavaScript в пользу .

В Ruby равенство under требует, чтобы оба операнда были одного типа, например false. Оператор является гибким и может быть определен произвольно для любого данного типа. Например, значение типа — это диапазон целых чисел, например . ложно, поскольку типы различны (диапазон или целое число); однако верно, т.к. по значениям означает «включение в диапазон». Согласно этой семантике, является несимметричным ; eg является ложным, поскольку оно интерпретируется скорее как означающее , чем .

Словарь синонимов

равно см. и Л все равноравновеликий, -весный, -действующий см. одинаковыйравновеликий, -весный, -действующий см. одинаковыйравновеликий, -весный, -действующий см. одинаковыйравнодушие см. хладнокровиеравнодушный см. беззаботный, бесстрастный, хладнокровныйравнозначащий, -именный см. одинаковыйравнозначащий, -именный см. одинаковыйравно как см. какравнолетки см. ровесникравномерность см. согласиеравномерный, -правный, -сильный, -ценный см. одинаковыйравномерный, -правный, -сильный, -ценный см. одинаковыйравномерный, -правный, -сильный, -ценный см. одинаковыйравномерный, -правный, -сильный, -ценный см. одинаковый

Alt-коды в помощь

Как поставить знак «Примерно равно» на клавиатуре? Как уже было сказано, пользователь не сможет ни при каких обстоятельствах отыскать соответствующий элемент на клавиатурной панели. Зато при желании можно без труда напечатать его посредством специализированных команд и кодов. Начнем с самого простого. Речь идет об Alt-кодах. Их иногда называют ASCII-кодами. С помощью специальных комбинаций продвинутые ПК-пользователи печатают различные уникальные символы. И знаки приблизительного равенства не являются исключением.

Чтобы осуществить их вставку в текст, потребуется:

1. Установить курсор-указатель мыши в предполагаемом месте появления знака.
2. Активировать режим «Нам Лок» на компьютере. Для этого обычно достаточно нажатия на клавишу Num Lock.
3. Нажать на клавишу Alt.
4. Напечатать код 8776 при помощи циферной клавиатуры. Она располагается в правой части клавиатурной панели.
5. Отпустить нажатые ранее клавиши.

Дело сделано. Символ «Примерно равно» будет установлен в указанном заранее месте. Подобный расклад на практике встречается все чаще. Он значительно упрощает жизнь продвинутым юзерам.

Важно: на клавиатуре можно увидеть разные кнопки «Альт». При работе с ASCII-кодами необходимо воспользоваться одной из соответствующий клавиш

Не важно, с какой стороны клавиатуры.

Бесконечное десятичное разложение

Для действительного числа x и целого числа n ≥ 0 пусть [ x ] _n обозначает (конечное) десятичное разложение наибольшего числа, которое не больше x , которое имеет ровно n цифр после десятичного знака. Пусть d _i обозначает последнюю цифру [ x ] _i . Несложно понять, что [ x ] _n можно получить, добавив d _n справа от [ x ] _{n –1} . Таким образом, есть

[ х ] _п = [ х ] . d ₁ d ₂ … d _{n −1} d _n ,

а разница [ x ] _{n –1} и [ x ] _n составляет

| [ x ] _n — [ x ] _{n –1} | = d _n ⋅ 10 — n <10 — n +1 ,

который либо равен 0, если d _n = 0, либо становится сколь угодно малым, когда n стремится к бесконечности. Согласно определению предела , x — это предел [ x ] _n, когда n стремится к бесконечности . Это записывается как или
Иксзнак равноLimп→∞Иксп{\ textstyle \; x = \ lim _ {n \ rightarrow \ infty} _ {n} \;}

х = [ х ] . д ₁ д ₂ … д _н …,

который называется бесконечное расширение десятичной из х .

И наоборот, для любого целого числа [ x ] и любой последовательности цифр (бесконечное) выражение x . d ₁ d ₂ … d _n … представляет собой бесконечное десятичное разложение действительного числа x . Это расширение уникально, если ни все d _n равны 9, ни все d _n равны 0 для достаточно большого n (для всех n больше некоторого натурального числа N ).
(dп)пзнак равно1∞{\ textstyle \; (d_ {n}) _ {n = 1} ^ {\ infty}}

Если все d _n для n > N равны 9 и [ x ] _n = [ x ] . d ₁ d ₂ … d _n , предел последовательности — это десятичная дробь, полученная заменой последней цифры, отличной от 9, то есть: d _N , на d _N + 1, и замены всех последующих 9 на 0 ( см. 0.999 … ).
(Иксп)пзнак равно1∞{\ textstyle \; ( _ {п}) _ {п = 1} ^ {\ infty}}

Любая такая десятичная дробь, т. Е. D _n = 0 для n > N , может быть преобразована в ее эквивалентное бесконечное десятичное разложение путем замены d _N на d _N — 1 и замены всех последующих нулей на 9 (см. 0.999 … ).

Таким образом, каждое действительное число, не являющееся десятичной дробью, имеет уникальное бесконечное десятичное расширение. Каждая десятичная дробь имеет ровно два бесконечных десятичных разложения, одно из которых содержит только 0 после некоторого места, что получается с помощью приведенного выше определения [ x ] _n , а другое, содержащее только 9 после некоторого места, которое получается путем определения [ x ] _n как самое большое число, которое меньше , чем х , имея в точности п цифр после десятичного знака.

Рациональное число

Деление в столбик позволяет вычислить бесконечное десятичное разложение рационального числа . Если рациональное число является , деление в конце концов прекращается, давая десятичное число, которое можно продолжить до бесконечности, добавив бесконечное количество нулей. Если рациональное число не является десятичной дробью, деление может продолжаться бесконечно. Однако, поскольку все последующие остатки меньше делителя, существует только конечное число возможных остатков, и после некоторого места одна и та же последовательность цифр должна бесконечно повторяться в частном. То есть есть повторяющаяся десятичная дробь . Например,

181 год = 0. 012345679 012 … (с неограниченно повторяющейся группой 012345679).

И наоборот, каждая в конечном итоге повторяющаяся последовательность цифр — это бесконечное десятичное разложение рационального числа. Это является следствием того факта, что повторяющаяся часть десятичного представления фактически представляет собой бесконечный геометрический ряд , сумма которого будет равна рациональному числу. Например,

0,0123123123…знак равно12310000∑kзнак равно∞0,001kзнак равно12310000 11-0,001знак равно1239990знак равно41 год3330{\ displaystyle 0,0123123123 \ ldots = {\ frac {123} {10000}} \ sum _ {k = 0} ^ {\ infty} 0,001 ^ {k} = {\ frac {123} {10000}} \ {\ frac {1} {1-0.001}} = {\ frac {123} {9990}} = {\ frac {41} {3330}}}

Где на клавиатуре знак приблизительно (примерно равно)?

На обычной клавиатуре знак

находится там же, где и буква Ё, только язык должен стоять английский. Сколько я не пыхтела, у меня так и не получилось набрать вот такой двойной знак приблизительно ≈ , поэтому можете его попросту скопировать и пользоваться на здоровье.

Конечно, для набора таких знаков существуют специальные буквенные комбинации. Для примерно равно это Alt (нажать и держать) + (в раскладке латиницей) 008776 (в такой же раскладке) и получится ≈.

Гораздо проще пойти в специальные знаки и найти значок там в шрифте Ариал (Arial), прокрути почти до самого конца:

А ещё проще скопировать здесь и держать закладку на этой странице. Поверьте, я так поступаю почти со всеми сложными знаками, потому что помнить комбинации и бесконечно искать в таблице — не самый удобный метод. Я замучилась с ними и считаю, что иногда быть блондинкой — просто полезно для здоровья и внутренней гармонии.

В математике довольно часто используется знак приблизительно (примерно равно), он выглядит следующим образом:

На клавишах клавиатуры знака приблизительно нет, тем не менее его всё же можно набрать с помощью клавиатуры.

Здесь нам помогут Alt-коды: данному знаку соответствует код 008776.

Ввести этот код нужно вот так:

1) Сначала нужно удостовериться, что у вас включена цифровая клавиатура (она активируется нажатием клавиши Num Lock).

2) Зажмите клавишу «Alt».

3) На цифровой клавиатуре поочерёдно введите шесть цифр: 0, 0, 8, 7, 7 и 6.

4) Отпустите клавишу «Alt».

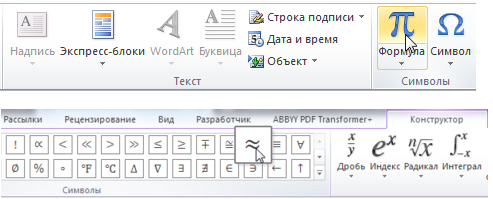
Если вы работаете в Ворде, то проще не набирать указанный Alt-код, а воспользоваться конструктором формул.

1) Откройте панель «Вставка» и нажмите на «Формула».

2) В документе появится «Место для формулы» и станет активной вкладка «Конструктор»: на этой вкладке в разделе «Символы» имеется знак «≈».

Также расскажу, как поставить знак приблизительно на клавиатуре Андроид (возможно, кому-нибудь окажется полезным).

1) Сначала переключитесь на специальную клавиатуру с цифрами и символами — для этого нажмите на «?123»:

2) Теперь нужно открыть список дополнительных символов — нажмите на «=

Знак , который написала пользователь Иринка — картинка при помощи клавиши Shift + клавиша с буквой Ё ( в английской раскладке ) — это знак » тильда » , который не означает знак » приблизительно равно » .

Есть очень простой способ поставить знак ≈ без клавиатуры . Достаточно нажать Пуск, затем Все программы , затем Стандартные — Служебные — Таблица символов . Найти там нужный вам знак ( в данном случае , знак » приблизительно равно » , то есть ≈ ) , скопировать его и вставить в нужный текст . И не нужно заморачиваться по поводу данного знака . А с клавишей Alt я не мог найти такой знак , а может я плохо искал .

Нет на клавиатуре такого знака (символа). «Примерно равно» — это две волнистые черточки, одна над другой расположенные. На клавиатуре же имеется только символ с одной такой черточкой. Тильдой называется, под Esc располагается. С буквой Ё одну клавишу делит.

На клавиатуре знака «приблизительно» («примерно») ни на одной из клавиш вы не обнаружите. Действительно, одинарный знак «

« под названием «тильда» на «клаве» имеется, а находится он на одной клавише с буковкой «Ё» (для его набора нужно сменить язык на английский). Но согласитесь, тильда — это совсем не то, что нам нужно.

И хотя значок «приблизительно» на клавиатуре не значится, его все-таки можно напечатать без сложных переходов через кнопку «Пуск». Для того чтобы изобразить значок нужно воспользоваться специальным числовым кодом.

Попробуйте в Ворде сделать следующее: зажимаем кнопку Alt и удерживаем её, а другой рукой выводим «+», а затем код «008776» и получаем искомый знак.

«Alt» + «+» + «008776» = «≈»

История появления

Знак равенства в современной форме создал валлийский математик Роберт Рекорд (Robert Recorde, ок. —) в своём труде The Whetstone of Witte («Оселок остроумия», 1557). Он обосновал применение двух параллельных штрихов так (орфография оригинала — ранненовоанглийский):

	And to auoide the tediouſe repetition of theſe woordes : is equalle to : I will ſette as I doe often in woorke vſe, a paire of paralleles, or Gemowe lines of one lengthe, thus: =, bicauſe noe .2. thynges, can be moare equalle.		И чтобы избежать утомительного повторения этих слов : является равным : я буду рисовать, как часто делаю в рабочем обиходе, пару параллелей, или линий-близнецов одной длины, таким образом: =, ибо никакие две вещи не могут быть более равными.
— The Whetstone of Witte

До этого в античной и средневековой математике равенство обозначалось словесно (например est egale). Как можно видеть на изображении страницы из книги Рекорда, введённый им знак равенства был значительно длиннее современного. В своих более ранних трудах в качестве символа равенства Рекорд использовал букву Z.

Абзац из The Whetstone of Witte, где вводится знак равенства

Первое печатное появление знака равенства в математической формуле (записано уравнение 14x+15=71{\displaystyle 14x+15=71})

Рене Декарт в XVII веке при записи стал использовать æ (от лат. aequalis), а современный знак равенства он использовал, чтобы указать, что коэффициент может быть отрицательным. Франсуа Виет знаком равенства обозначал вычитание. Символ Рекорда получил распространение далеко не сразу. В континентальной Европе знак «=» был введён Лейбницем только на рубеже XVII—XVIII веков, то есть более чем через 100 лет после смерти впервые использовавшего его для этого Роберта Рекорда.

Самые необходимые знаки на клавиатуре

Ни один пользователь компьютера или ноутбука не обойдется без буквенных знаков на клавиатуре, вводимых с помощью соответствующих клавиш. Почти на каждой клавише обозначены 2 буквы – английская вверху и русская внизу, т.е. на клавиатуре есть 26 букв английского алфавита и 33 буквы русского. Причем это могут быть как строчные буквы, так и прописные, которые печатаются с помощью клавиши Shift.

Знаки препинания есть и в английской, и в русской раскладке, хотя и находятся в разных местах клавиатуры. Удобно при работе с русским текстом, что точка и запятая – это одна и та же клавиша, которая находится в нижнем ряду буквенных клавиш самой последней. Только запятая печатается в комбинации с клавишей с Shift. А в английской раскладке точка – клавиша с русской буквой Ю, а запятая – Б. Так что для ввода данных знаков препинания не нужно переключаться с одного шрифта на другой.

Цифровые знаки или цифры мы используем не только для вычислений, но и в тексте для обозначения различных числовых данных. При этом можно пользоваться как верхним цифровым рядом клавиатуры, так и дополнительным цифровым блоком (малая цифровая клавиатура), находящимся у клавиатуры справа.

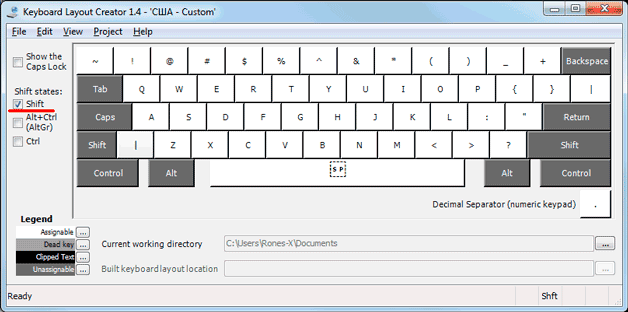
Основные знаки арифметических действий (плюс «+», минус «-», умножение «*», деление «/»), расположенные на малой цифровой клавиатуре по аналогии с привычным калькулятором, поэтому ими удобно пользоваться при расчетах. А вот если Вам нужно именно напечатать знак равно «=», а не узнать результат вычислений, то такого знака Вы там не найдете. Он находится в верхнем цифровом ряду после цифры 0 через одну клавишу.

Словарь антонимов

РАВНОДУШИЕ — НЕРАВНОДУШИЕИспытывать равнодушие к происходящему — чувствовать неравнодушие к происходящему. Свидетельство равнодушия — свидетельство неравнодушия.БЕЗУЧАСТИЕ — СОЧУВСТВИЕБезучастный — сочувственныйбезучастно — сочувственнобезучастность — сочувствие— Что может быть страшнее докторского безучастия! — Вас только что обидело сочувствие, и вдруг я стал безучастным. Федин. Санаторий Арктур.БЕЗУЧАСТНОСТЬ — СОЧУВСТВИЕПроявить безучастность — проявить сочувствие. Ο Девушка поняла, что я сын умершего человека, и смотрела на меня не с посторонней безучастностью, а с сочувствием. Н. Евдокимов. Страстная площадь.НЕЧУВСТВИТЕЛЬНОСТЬ — ЧУВСТВИТЕЛЬНОСТЬНу да, это только — «чувствительность кожи» — и всегда связанная с внешней чувствительностью — нечувствительность внутренняя, душевная слепота. Блок. Дневник, 9 янв. 1912.БЕСЧУВСТВЕННОСТЬ — ЧУВСТВОСтраннее всего, что все, что мы можем сказать о личности, ограничивается тем, что она ничтожна перед чувством, разумом, волею, добродетелью, красотой и тому подобными вечными и непреходящими идеями, но что без нее, преходящего и случайного явления, не было бы ни чувства, ни ума, ни воли, ни добродетели, ни красоты, так же как не было бы ни бесчувственности, ни глупости, ни бесхарактерности, ни порока, ни безобразия. Белинский. Взгляд на русскую литературу 1846 года.РАВНОДУШНЫЙ — НЕРАВНОДУШНЫЙРавнодушно — неравнодушноравнодушие — неравнодушиеРавнодушный человек — неравнодушный человек. Равнодушный взгляд — неравнодушный взгляд. Равнодушен к музыке — неравнодушен к музыке. Равнодушное отношение — неравнодушное отношение. Ο Вы заставляете предполагать в вас такую преданность, к которой нельзя оставаться равнодушной. Не все же нам одним быть неравнодушными. А. Островский. Бешеные деньги. С ранних лет и до преклонных, Безотрадных лет, Был к нему неравнодушен Равнодушный свет. Полонский. Памяти Ф.И. Тютчева.РАВНОДУШНЫЙ — ОТЗЫВЧИВЫЙРавнодушно — отзывчиворавнодушие — отзывчивостьРавнодушный человек — отзывчивый человек. Ο Именно от душевного благополучия зависит, будут ли дети непринужденными или скованными, искренними или скрытными, равнодушными или отзывчивыми, добрыми или злыми. В. Аграновский. Вниз по лестнице. Волны поклонения бурлили вокруг Багратиона. Но он не слышал их шума, холодно равнодушный к восторженным похвалам и горячо отзывчивый на всякое искреннее слово. С. Голубов. Багратион.РАВНОДУШНЫЙ — НЕРАВНОДУШНЫЙРавнодушно — неравнодушноравнодушие — неравнодушиеРавнодушный человек — неравнодушный человек. Равнодушный взгляд — неравнодушный взгляд. Равнодушен к музыке — неравнодушен к музыке. Равнодушное отношение — неравнодушное отношение. Ο Вы заставляете предполагать в вас такую преданность, к которой нельзя оставаться равнодушной. Не все же нам одним быть неравнодушными. А. Островский. Бешеные деньги. С ранних лет и до преклонных, Безотрадных лет, Был к нему неравнодушен Равнодушный свет. Полонский. Памяти Ф.И. Тютчева.РАВНОДУШНЫЙ — ОТЗЫВЧИВЫЙРавнодушно — отзывчиворавнодушие — отзывчивостьРавнодушный человек — отзывчивый человек. Ο Именно от душевного благополучия зависит, будут ли дети непринужденными или скованными, искренними или скрытными, равнодушными или отзывчивыми, добрыми или злыми. В. Аграновский. Вниз по лестнице. Волны поклонения бурлили вокруг Багратиона. Но он не слышал их шума, холодно равнодушный к восторженным похвалам и горячо отзывчивый на всякое искреннее слово. С. Голубов. Багратион.РАВНОДУШНЫЙ — НЕРАВНОДУШНЫЙРавнодушно — неравнодушноравнодушие — неравнодушиеРавнодушный человек — неравнодушный человек. Равнодушный взгляд — неравнодушный взгляд. Равнодушен к музыке — неравнодушен к музыке. Равнодушное отношение — неравнодушное отношение. Ο Вы заставляете предполагать в вас такую преданность, к которой нельзя оставаться равнодушной. Не все же нам одним быть неравнодушными. А. Островский. Бешеные деньги. С ранних лет и до преклонных, Безотрадных лет, Был к нему неравнодушен Равнодушный свет. Полонский. Памяти Ф.И. Тютчева.РАВНОДУШНЫЙ — ОТЗЫВЧИВЫЙРавнодушно — отзывчиворавнодушие — отзывчивостьРавнодушный человек — отзывчивый человек. Ο Именно от душевного благополучия зависит, будут ли дети непринужденными или скованными, искренними или скрытными, равнодушными или отзывчивыми, добрыми или злыми. В. Аграновский. Вниз по лестнице. Волны поклонения бурлили вокруг Багратиона. Но он не слышал их шума, холодно равнодушный к восторженным похвалам и горячо отзывчивый на всякое искреннее слово. С. Голубов. Багратион.

Стандартные средства «Виндовс»

Как поставить знак «Примерно равно»? Этот символ предлагается печатать в тексте по-разному. Второй вариант — это использование службы «Виндовс» под названием «Таблица символов». Данная утилита помогает вставлять, копировать и изучать все возможные специальные знаки. И математические символы в том числе.

Руководство по воплощению задумки в жизнь будет иметь такую интерпретацию:

1. Зайти в службу «Таблица символов». Ее можно отыскать через «Пуск» в папке «Стандартные» — «Служебные».
2. Внимательно изучить появившееся окно. Кликнуть по иконке с волнистым равно.
3. Нажать на элемент управления под названием «Выбрать». В качестве альтернативы можно дважды кликнуть по изображению символики левой кнопкой мыши.
4. Выбрать команду «Копировать» в нижней части окна.
5. Вставить в текст скопированный знак «Примерно равно» из буфера обмена в текстовый документ любым удобным способом.

Дело сделано. Как показывает практика, этот вариант развития событий встречается не слишком часто, но он имеет место. Что еще можно предложить пользователям?

Таблица математических знаков (символов) эквивалентности с кодами Unicode

Математические знаки (символы) эквивалентности

знак	Unicode значение	Название знака		знак	Unicode значение	Название знака
=		равно	≠		не равно
≃		асимптотически равно	≄		асимптотически не равно
≅		конгруэнтность (геометрическое равенство)	≆
			≇
≌		конгруэнтность	≂
≈		примерно равно	≉
∝		пропорционально
≡		идентично, тождество	≢		не идентично
≊		равно или почти равно	≋		тройная тильда, конгруэнтность
≍		эквивалентно	≣		строго эквивалентно
≎			≏
≐		округлённо равно	≑
≒		обратное преобразование Лапласа	≓		прямое преобразование Лапласа
≔		присваивание	≕
≘		соответствует	≚
≗			≙		соответствует
≞			≟		может быть равно
≜		Равно по определению	≝		Равно по определению
≛			≖

Происхождение

Десять пальцев на двух руках, возможное происхождение десятичного счета

Многие системы счисления древних цивилизаций используют десять и его силы для представления чисел, возможно потому, что на двух руках десять пальцев, и люди начали считать, используя свои пальцы. Примерами являются цифры Брахми , греческие цифры , еврейские цифры , римские цифры и китайские цифры . Очень большие числа было трудно представить в этих старых системах счисления, и только лучшие математики могли умножать или делить большие числа. Эти трудности были полностью решены с введением индийско-арабской системы счисления для представления целых чисел . Эта система была расширена для представления некоторых нецелочисленных чисел, называемых или десятичными числами , для формирования десятичной системы счисления .